
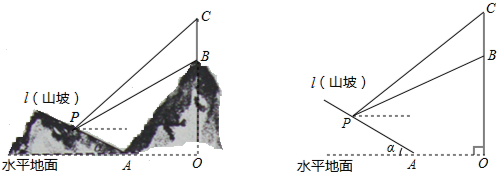
分析 (1)过点P作PD⊥OC于D,PE⊥OA于E,则四边形ODPE为矩形,先解Rt△PBD,得出BD=PD•tan26.6°;解Rt△CPD,得出CD=PD•tan31°;再根据CD-BD=BC,列出方程,求出PD=400即可求得点P到OC的距离;
(2)利用求得的线段PD的长求出PE=40,AE=100,然后在△APE中利用三角函数的定义即可求解.
解答 解:(1)如图,过点P作PD⊥OC于D,PE⊥OA于E,则四边形ODPE为矩形.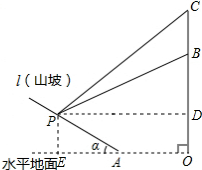
在Rt△PBD中,∵∠BDP=90°,∠BPD=26.6°,
∴BD=PD•tan∠BPD=PD•tan26.6°;
在Rt△CPD中,∵∠CDP=90°,∠CPD=31°,
∴CD=PD•tan∠CPD=PD•tan31°;
∵CD-BD=BC,
∴PD•tan31°-PD•tan26.6°=40,
∴0.60PD-0.50PD=40,
解得PD=400(米),
∴P到OC的距离为400米;
(2)在Rt△PBD中,BD=PD•tan26.6°≈400×0.50=200(米),
∵OB=240米,
∴PE=OD=OB-BD=40米,
∵OE=PD=400米,
∴AE=OE-OA=400-300=100(米),
∴tanα=$\frac{PE}{AE}$=$\frac{40}{100}$=0.4,
∴坡度为0.4.
点评 本题考查了解直角三角形的应用-仰角俯角问题、坡度坡角问题,难度适中,通过作辅助线,构造直角三角形,利用三角函数求解是解题的关键.


科目:初中数学 来源: 题型:解答题
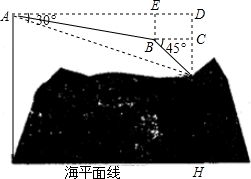 2015年4月25日,尼泊尔发生强烈地震,中国西藏部分地区也被波及,我国空军派出直升飞机“直九”抢险救灾,在一次执行运送药品及食品的任务时,“直九”军机飞行高度已知稳定在3500米,到达航线A出时测得樟木边防站M的俯角为26.5°,保持航向不变前行1700米到达E处,再匀速垂直下降500米到达B处后,测得边防站M的俯角为45°,计算:
2015年4月25日,尼泊尔发生强烈地震,中国西藏部分地区也被波及,我国空军派出直升飞机“直九”抢险救灾,在一次执行运送药品及食品的任务时,“直九”军机飞行高度已知稳定在3500米,到达航线A出时测得樟木边防站M的俯角为26.5°,保持航向不变前行1700米到达E处,再匀速垂直下降500米到达B处后,测得边防站M的俯角为45°,计算:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
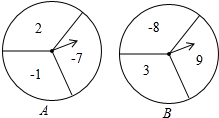 如图,两个可以自由转动的均匀转盘,A、B都被平均分成了3份,并在每份内标有一个有理数.有如下游戏规则:
如图,两个可以自由转动的均匀转盘,A、B都被平均分成了3份,并在每份内标有一个有理数.有如下游戏规则:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com