
【题目】二次函数y=ax2+bx+c(a>0)的顶点为P,其图像与x轴有两个交点A(﹣m,0),B(1,0),交y轴于点C(0,﹣3am+6a),以下说法:
①m=3;
②当∠APB=120°时,a= ![]() ;
;
③当∠APB=120°时,抛物线上存在点M(M与P不重合),使得△ABM是顶角为120°的等腰三角形;
④抛物线上存在点N,当△ABN为直角三角形时,有a≥ ![]()
正确的是( )
A.①②
B.③④
C.①②③
D.①②③④
【答案】D
【解析】解:①∵点A(﹣m,0)、B(1,0)在抛物线y=ax2+bx+c上,
∴ ![]() ,
,
由①﹣②得
am2﹣bm﹣a﹣b=0,
即(m+1)(am﹣a﹣b)=0.
∵A(﹣m,0)与B(1,0)不重合,
∴﹣m≠1即m+1≠0,
∴m= ![]() ,
,
∴点C的坐标为(0,3a﹣3b),
∵点C在抛物线y=ax2+bx+c上,
∴c=3a﹣3b,
代入②得a+b+3a﹣3b=0,即b=2a,
∴m= ![]() =3,故①正确;
=3,故①正确;
②∵m=3,∵A(﹣3,0),
∴抛物线的解析式可设为y=a(x+3)(x﹣1),
则y=a(x2+2x﹣3)=a(x+1)2﹣4a,
∴顶点P的坐标为(﹣1,﹣4a).
根据对称性可得PA=PB,
∴∠PAB=∠PBA=30°.
设抛物线的对称轴与x轴的交点为G,
则有PG⊥x轴,
∴PG=AGtan∠PAG=2× ![]() =
= ![]() ,
,
∴4a= ![]() ,
,
∴a= ![]() ,故②正确;
,故②正确;
③在第一象限内作∠MBA=120°,且满足BM=BA,过点M作MH⊥x轴于H,如图1,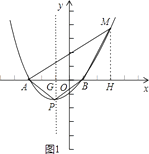
在Rt△MHB中,∠MBH=60°,
则有MH=4sin60°=4× ![]() =2
=2 ![]() ,BH=4cos60°=4×
,BH=4cos60°=4× ![]() =2,
=2,
∴点M的坐标为(3,2 ![]() ),
),
当x=3时,y= ![]() (3+3)(3﹣1)=2
(3+3)(3﹣1)=2 ![]() ,
,
∴点M在抛物线上,故③正确;
④∵点N在抛物线上,∴∠ABN≠90°,∠BAN≠90°.
当△ABN为直角三角形时,∠ANB=90°,
此时点N在以AB为直径的⊙G上,
因而点N在⊙G与抛物线的交点处,
要使点N存在,点P必须在⊙G上或⊙G外,如图2,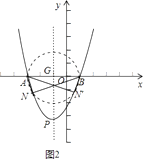
则有PG≥2,即4a≥2,也即a≥ ![]() ,故④正确.
,故④正确.
故选D.
①把A、B两点的坐标分别代入抛物线的解析式得到①式和②式,将两式相减即可得到m= ![]() ,即可得到C(0,3a﹣3b),从而得到c=3a﹣3b,代入②式,就可解决问题;
,即可得到C(0,3a﹣3b),从而得到c=3a﹣3b,代入②式,就可解决问题;
②设抛物线的对称轴与x轴的交点为G,则有PG⊥x轴,只需求出点P的坐标就可解决问题;
③在第一象限内作∠MBA=120°,且满足BM=BA,过点M作MH⊥x轴于H,如图1,只需求出点M的坐标,然后验证点M是否在抛物线上,就可解决问题;
④易知点N在抛物线上且△ABN为直角三角形时,只能∠ANB=90°,此时点N在以AB为直径的⊙G上,因而点N在⊙G与抛物线的交点处,要使点N存在,点P必须在⊙G上或⊙G外,如图2,只需根据点与圆的位置关系就可解决问题.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
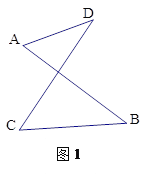
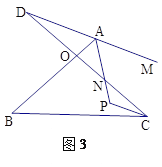
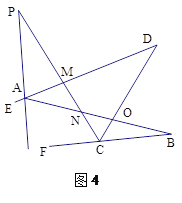
已知:如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”,试解答下列问题:
问题一:在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系 ;
问题二:在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N,试求∠P的度数;
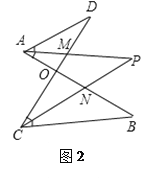
问题三:在图3中,已知AP、CP分别平分∠BAM、∠BCD,请问∠P与∠B、∠D之间存在着怎样的数量关系?并说明理由.
问题四:在图4中,已知AP的反向延长线平分∠EAB,CP平分∠DCF,请直接写出∠P与∠B、∠D之间的数量关系 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x,![]() 的方程组
的方程组![]() ,给出下列结论:①
,给出下列结论:①![]() 是方程组的解;②无论a取何值, x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4﹣a的解;④
是方程组的解;②无论a取何值, x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4﹣a的解;④![]() ,
,![]() 都为自然数的解有4对.其中正确的为______________.
都为自然数的解有4对.其中正确的为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个自然数m,若将其数字重新排列可得一个新的自然数n,如果m=3n,我们称m是一个“希望数”.例如:3105=3×1035,71253=3×23751,371250=3×123750.
(1)请说明41不是希望数,并证明任意两位数都不可能是“希望数”.
(2)一个四位“希望数”M记为![]() ,已知
,已知![]() ,且c=2,请求出这个四位“希望数”.
,且c=2,请求出这个四位“希望数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=60°,作边长为1的正六边形A1B1C1D1E1F1 , 边A1B1、F1E1分别在射线OM、ON上,边C1D1所在的直线分别交OM、ON于点A2、F2 , 以A2F2为边作正六边形A2B2C2D2E2F2 , 边C2D2所在的直线分别交OM、ON于点A3、F3 , 再以A3F3为边作正六边形A3B3C3D3E3F3 , …,依此规律,经第n次作图后,点Bn到ON的距离是 . 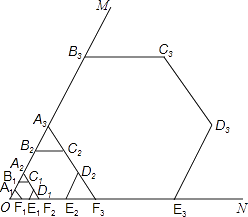
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片ABCD沿EF翻折,点A恰好落在BC边的A′处,若AB= ![]() ,∠EFA=60°,则四边形A′B′EF的周长是( )
,∠EFA=60°,则四边形A′B′EF的周长是( ) 
A.1+3 ![]()
B.3+ ![]()
C.4+ ![]()
D.5+ ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com