[题目]如图.∠MON=60°.作边长为1的正六边形A1B1C1D1E1F1 . 边A1B1.F1E1分别在射线OM.ON上.边C1D1所在的直线分别交OM.ON于点A2.F2 . 以A2F2为边作正六边形A2B2C2D2E2F2 . 边C2D2所在的直线分别交OM.ON于点A3.F3 . 再以A3F3为边作正六边形A3B3C3D3E3F3 . -.依此规律.经第n次作图后.点Bn到O 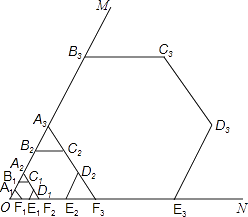题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，∠MON=60°，作边长为1的正六边形A1B1C1D1E1F1 ，边A1B1、F1E1分别在射线OM、ON上，边C1D1所在的直线分别交OM、ON于点A2、F2 ，以A2F2为边作正六边形A2B2C2D2E2F2 ，边C2D2所在的直线分别交OM、ON于点A3、F3 ，再以A3F3为边作正六边形A3B3C3D3E3F3 ， …，依此规律，经第n次作图后，点Bn到ON的距离是．

【答案】3n﹣1?
【解析】解：点B1到ON的距离是，点B2到ON的距离是3 ，
点B3到ON的距离是9 ，
点B4到ON的距离是27 ，
…
点Bn到ON的距离是3n﹣1 ．

首先求出B1 ， B2 ， B3 ， B4到ON的距离，条件规律后，利用规律解决问题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

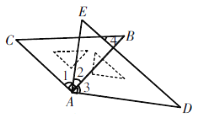
【题目】将一副三角板按如图放置，则下列结论：

①如果∠2=30°，则有AC∥DE；

②∠BAE+∠CAD =180°；

③如果BC∥AD，则有∠2=45°；

④如果∠CAD=150°，必有∠4=∠C；

正确的有( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】二次函数y=ax2+bx+c（a＞0）的顶点为P，其图像与x轴有两个交点A（﹣m，0），B（1，0），交y轴于点C（0，﹣3am+6a），以下说法：
①m=3；
②当∠APB=120°时，a= ；
③当∠APB=120°时，抛物线上存在点M（M与P不重合），使得△ABM是顶角为120°的等腰三角形；
④抛物线上存在点N，当△ABN为直角三角形时，有a≥
正确的是（）
A.①②
B.③④
C.①②③
D.①②③④

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，△ABC在直角坐标系中，

（1）△ABC中任意一点M(a,b)经过平移后的对应点为M′(a+2,b+1)，将△ABC作同样的平移,得到△A′B′C′，写出A′、B′、C′的坐标，并在图中画出平移后图形．

（2）求出三角形ABC的面积．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】下列调查中，适合用全面调查方式的是（）

A.调查“神舟十一号”飞船重要零部件的产品质量B.调查某电视剧的收视率

C.调查一批炮弹的杀伤力D.调查一片森林的树木有多少棵

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在平面直角坐标系中，以任意两点P（x1，y1）、Q（x2，y2）为端点的线段的中点坐标为．

（1）如图（1），C为线段AB中点，A点坐标为（0，4），B点坐标为（5，4），则点C的坐标为　　

（2）如图（2），F为线段DE中点，D点坐标为（﹣4，﹣3），E点坐标为（1，﹣3）．则点F的坐标为________

应用：

（1）如图（3），长方形ONDF的对角线相交于点M，ON，OF分别在x轴和y轴上，O为坐标原点，点D的坐标为（4，3），则点M的坐标为　　；

（2）在直角坐标系中，有A（﹣1，2），B（3，1），C（1，4）三点，另有一点D与A，B，C构成平行四边形的顶点，直接写出D的坐标．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】探究规律：我们有可以直接应用的结论：若两条直线平行，那么在一条直线上任取一点，无论这点在直线的什么位置，这点到另一条直线的距离均相等.例如：如图1，两直线∥，两点，在上，⊥于，⊥于，则.

如图2，已知直线∥，，为直线上的两点，.为直线上的两点.

（1）请写出图中面积相等的各对三角形： .

（2）如果，，为三个定点，点在上移动，那么无论点移动到任何位置，总有：与的面积相等；理由是： .

解决问题：

如图3，五边形是张大爷十年前承包的一块土地的示意图，经过多年开垦荒地，现已变成如图4所示的形状，但承包土地与开垦荒地的分界小路（图4中折线）还保留着，张大爷想过点修一条直路，直路修好后，要保持直路左边的土地面积与承包时的一样多.请你用以上的几何知识，按张大爷的要求设计出修路方案.（不计分界小路与直路的占地面积）