
【题目】探究规律:我们有可以直接应用的结论:若两条直线平行,那么在一条直线上任取一点,无论这点在直线的什么位置,这点到另一条直线的距离均相等.例如:如图1,两直线![]() ∥
∥![]() ,两点
,两点![]() ,
,![]() 在
在![]() 上,
上,![]() ⊥
⊥![]() 于
于![]() ,
,![]() ⊥
⊥![]() 于
于![]() ,则
,则![]() .
.
如图2,已知直线![]() ∥
∥![]() ,
,![]() ,
,![]() 为直线
为直线![]() 上的两点,
上的两点,![]() .
.![]() 为直线
为直线![]() 上的两点.
上的两点.
(1)请写出图中面积相等的各对三角形: .
(2)如果![]() ,
,![]() ,
,![]() 为三个定点,点
为三个定点,点![]() 在
在![]() 上移动,那么无论
上移动,那么无论![]() 点移动到任何位置,总有: 与
点移动到任何位置,总有: 与![]() 的面积相等;理由是: .
的面积相等;理由是: .

解决问题:
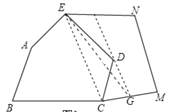
如图3,五边形![]() 是张大爷十年前承包的一块土地的示意图,经过多年开垦荒地,现已变成如图4所示的形状,但承包土地与开垦荒地的分界小路(图4中折线
是张大爷十年前承包的一块土地的示意图,经过多年开垦荒地,现已变成如图4所示的形状,但承包土地与开垦荒地的分界小路(图4中折线![]() )还保留着,张大爷想过点
)还保留着,张大爷想过点![]() 修一条直路,直路修好后,要保持直路左边的土地面积与承包时的一样多.请你用以上的几何知识,按张大爷的要求设计出修路方案.(不计分界小路与直路的占地面积)
修一条直路,直路修好后,要保持直路左边的土地面积与承包时的一样多.请你用以上的几何知识,按张大爷的要求设计出修路方案.(不计分界小路与直路的占地面积)
(1)写出设计方案,并在图4中画出相应的图形;
(2)说明方案设计理由.
【答案】探究规律:(1)![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() ;(2)
;(2)![]() ; 同底等高的两个三角形的面积相等;解决问题:(1)方案见解析;(2)理由见解析.
; 同底等高的两个三角形的面积相等;解决问题:(1)方案见解析;(2)理由见解析.
【解析】分析:(1)根据同底等高的三角形的面积相等与三角形的面积的和差关系求解;(2)①结合三角形的面积公式回答;②根据平行线间的距离处处相等和同底等高的两三角形面积相等设计方案.
详解:(1)![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() .
.
(2)![]() ;同底等高的两个三角形的面积相等.
;同底等高的两个三角形的面积相等.
连接![]() ,过
,过![]() 点作
点作![]() 的平行线
的平行线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
![]() 就是所求的道路.
就是所求的道路.
设EF交CD于点H,
∵EC∥DF,
∴D和F点到EC的距离相等(平行线间的距离处处相等),
又∵EC=EC,
∴S△ECF=S△ECD(同底等高的两三角形面积相等),
∴S五边形ABCDE=S五边形EDCMN,S五边形EDCMN=S四边形EFMN.
即:EF为直路的位置可以保持直路左边的土地面积与承包时的一样多,右边的土地面积与开垦的荒地面积一样多


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】一个自然数m,若将其数字重新排列可得一个新的自然数n,如果m=3n,我们称m是一个“希望数”.例如:3105=3×1035,71253=3×23751,371250=3×123750.
(1)请说明41不是希望数,并证明任意两位数都不可能是“希望数”.
(2)一个四位“希望数”M记为![]() ,已知
,已知![]() ,且c=2,请求出这个四位“希望数”.
,且c=2,请求出这个四位“希望数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=60°,作边长为1的正六边形A1B1C1D1E1F1 , 边A1B1、F1E1分别在射线OM、ON上,边C1D1所在的直线分别交OM、ON于点A2、F2 , 以A2F2为边作正六边形A2B2C2D2E2F2 , 边C2D2所在的直线分别交OM、ON于点A3、F3 , 再以A3F3为边作正六边形A3B3C3D3E3F3 , …,依此规律,经第n次作图后,点Bn到ON的距离是 . 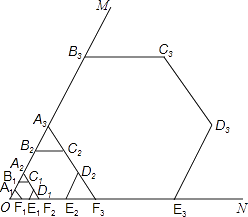
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是( )

A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE;

(1)求证:△ACD≌△BCE;
(2)若∠D=50°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间关系的图像如图所示.根据图像解答下列问题:
(1)谁先出发?先出发多少时间?谁先到达终点?先到多少时间?
(2)分别求出甲、乙两人的行驶速度;
(3)在什么时间段内,两人均行驶在途中?(不包括起点和终点)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片ABCD沿EF翻折,点A恰好落在BC边的A′处,若AB= ![]() ,∠EFA=60°,则四边形A′B′EF的周长是( )
,∠EFA=60°,则四边形A′B′EF的周长是( ) 
A.1+3 ![]()
B.3+ ![]()
C.4+ ![]()
D.5+ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只蚂蚁在一个半圆形的花坛的周边寻找食物,如图1,蚂蚁从圆心O出发,按图中箭头所示的方向,依次爬完下列三条线路:(1)线段OA、(2)半圆弧AB、(3)线段BO后,回到出发点。已知蚂蚁在爬行过程中保持匀速,且在寻找到食物后停下来吃了2分钟。蚂蚁离出发点的距离s(蚂蚁所在位置与O点之间线段的长度)与时间t之间的图象如图2所示,问:
(1)花坛的半径是_______米,蚂蚁是在上述三条线路中的哪条上寻找到了食物_________(填(1)、(2)、或(3));
(2)蚂蚁的速度是_______米/分钟;

(3)蚂蚁从O点出发,直到回到O点,一共用时多少分钟?(![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com