
【题目】如图,△ABC在直角坐标系中,
(1)△ABC中任意一点M(a,b)经过平移后的对应点为M′(a+2,b+1),将△ABC作同样的平移,得到△A′B′C′,写出A′、B′、C′的坐标,并在图中画出平移后图形.
(2)求出三角形ABC的面积.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商场第1次用39万元购进A、B两种商品,销售完后获得利润6万元,它们的进价和售价如下表:(总利润=单件利润×销售量)
商品 价格 | A | B |
进价(元/件) | 1200 | 1000 |
售价(元/件) | 1350 | 1200 |
(1)该商场第1次购进A、B两种商品各多少件?
(2)商场第2次以原价购进A、B两种商品,购进A商品的件数不变,而购进B商品的件数是第1次的2倍,A商品按原价销售,而B商品打折销售,若两种商品销售完毕,要使得第2次经营活动获得利润等于54000元,则B种商品是打几折销售的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
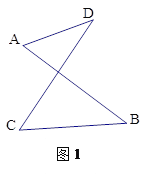
已知:如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”,试解答下列问题:
问题一:在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系 ;
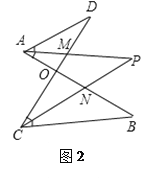
问题二:在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N,试求∠P的度数;
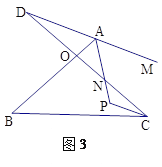
问题三:在图3中,已知AP、CP分别平分∠BAM、∠BCD,请问∠P与∠B、∠D之间存在着怎样的数量关系?并说明理由.
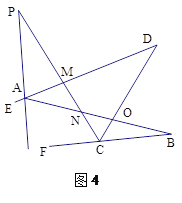
问题四:在图4中,已知AP的反向延长线平分∠EAB,CP平分∠DCF,请直接写出∠P与∠B、∠D之间的数量关系 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个自然数m,若将其数字重新排列可得一个新的自然数n,如果m=3n,我们称m是一个“希望数”.例如:3105=3×1035,71253=3×23751,371250=3×123750.
(1)请说明41不是希望数,并证明任意两位数都不可能是“希望数”.
(2)一个四位“希望数”M记为![]() ,已知
,已知![]() ,且c=2,请求出这个四位“希望数”.
,且c=2,请求出这个四位“希望数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=60°,作边长为1的正六边形A1B1C1D1E1F1 , 边A1B1、F1E1分别在射线OM、ON上,边C1D1所在的直线分别交OM、ON于点A2、F2 , 以A2F2为边作正六边形A2B2C2D2E2F2 , 边C2D2所在的直线分别交OM、ON于点A3、F3 , 再以A3F3为边作正六边形A3B3C3D3E3F3 , …,依此规律,经第n次作图后,点Bn到ON的距离是 . 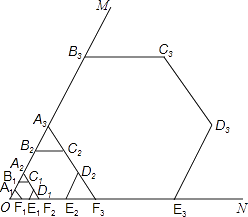
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE;

(1)求证:△ACD≌△BCE;
(2)若∠D=50°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,顶点A、B的坐标分别是A(1,0),B(0,﹣2),顶点C、D在双曲线y=![]() 上,边AD与y轴相交于点E,S四边形BEDC=5S△ABE=10,则k的值是( )
上,边AD与y轴相交于点E,S四边形BEDC=5S△ABE=10,则k的值是( )
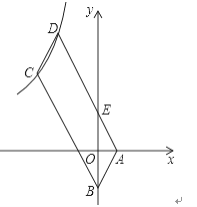
A. -16 B. -9 C. -8 D. -12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com