
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 如果设A点关于y轴的对称点为A′,那么C点就是A′B与y轴的交点.易知A′(-3,3),又B(1,0),可用待定系数法求出直线A′B的方程.再求出C点坐标,根据勾股定理分别求出AC、BC的长度.那么小球路线从A点到B点经过的路线长是AC+BC,从而得出结果.
解答 解:如果将y轴当成平面镜,设A点关于y轴的对称点为A′,则由小球路线知识可知,A′相当于A的像点,光线从A到C到B,相当于小球路线从A′直接到B,所以C点就是A′B与y轴的交点.
∵A点关于y轴的对称点为A′,A(3,3),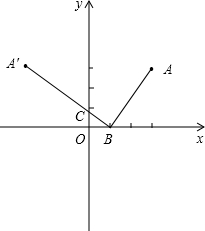
∴A′(-3,3),
进而由两点式写出A′B的直线方程为:y=-$\frac{3}{4}$(x-1).
令x=0,求得y=$\frac{3}{4}$.所以C点坐标为(0,$\frac{3}{4}$).
那么根据勾股定理,可得:
AC=$\sqrt{(3-\frac{3}{4})^{2}+{3}^{2}}=\frac{15}{4}$,BC=$\sqrt{(\frac{3}{4})^{2}+{1}^{2}}=\frac{5}{4}$.
因此,AC+BC=5.
故选B.
点评 此题考查轴对称的基本性质,勾股定理的应用等知识点.关键是根据小球路线从A点到B点经过的路线长是AC+BC.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源:2016-2017学年江西省下期九年级第一次月考数学试卷(解析版) 题型:判断题
如图,在平面直角坐标系xOy中,点A(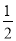 ,2),B(3,n)在反比例函数y=
,2),B(3,n)在反比例函数y=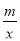 (m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点C,过点A的直线l与x轴的交点为D(1,0),过点C作CE∥x轴交直线l于点E.
(m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点C,过点A的直线l与x轴的交点为D(1,0),过点C作CE∥x轴交直线l于点E.
(1)求m的值,并求直线l对应的函数表达式;
(2)求点E的坐标;
(3)过点B作射线BN∥x轴,与AE交于点M(补全图形),求证:tan∠ABN=tan∠CBN.

查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省七年级下学期第一次月考数学试卷(解析版) 题型:解答题
简便计算:
(1)123452﹣12344×12346.
(2)3.76542+0.4692×3.7654+0.23462.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com