
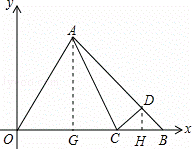
已知:在△AOB中,AB= ,OB=6,∠B=45°,以O为原点,所在直线为x轴建立直角坐标系
,OB=6,∠B=45°,以O为原点,所在直线为x轴建立直角坐标系
(1)写出点A的坐标:;
(2)C为线段OB上的动点,D为线段AB上的动点,且始终有CD∥OA,若C由O向B运动的距离OC=x,△ACD的面积为y
①求y与x之间的函数关系式;
②是否存在这样的点D,使△AOC的面积等于△ACD的面积的2倍?若存在,请求出点D的坐标,否则请说明理由.

解:(1)过点A作AG⊥x轴于点G,则∠AGB=90°.
在Rt△ABG中,∵∠AGB=90°,AB=4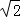 ,∠B=45°,
,∠B=45°,
∴AG=BG=4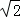 ×
×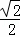 =4,
=4,
∴OG=OB﹣BG=6﹣4=2,
∴点A的坐标为 (2,4).
(2,4).
故答案为(2,4);
(2)①过点D作DH⊥x轴于点H.
∵CD∥OA,
∴△BCD∽△BOA,
∴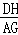 =
=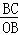 ,即
,即 =
= ,
,
∴DH=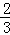 (6﹣x).
(6﹣x).
∵S△ACD=S△ABC﹣S△BCD=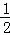 BC
BC •AG﹣
•AG﹣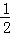 BC•DH,
BC•DH,
∴y=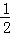 (6﹣x)×4﹣
(6﹣x)×4﹣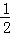 (6﹣x)•
(6﹣x)•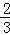 (6﹣x)=﹣
(6﹣x)=﹣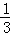 x2+2x,
x2+2x,
即y与x之间的函数关系式为y=﹣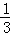 x2+2x;
x2+2x;
②存在这样的点D,能够使△AOC的面积等于△ACD的面积的2倍.
∵S△AOC=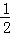 OC•AG=
OC•AG=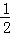 x×4=2x,
x×4=2x,
∴2x=2(﹣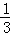 x2+2x),
x2+2x),
整理,得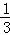 x2﹣x=0,
x2﹣x=0,
解得x1=3,x2=0(不合题意舍去),
∴x=3.
当x=3时,BH=DH=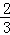 (6﹣x)=
(6﹣x)=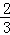 ×(6﹣3)=2,
×(6﹣3)=2,
∴OH=OB﹣BH=6﹣2=4,
∴点D的坐标为(4,2).
点


科目:初中数学 来源: 题型:
用配方法解方程x2+6x﹣5=0时,此方程可变形为()
A. (x+3)2=14 B. (x﹣3)2=14 C. (x+3)2=11 D. (x+6)2=14
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,平行四边形ABCD中,AB=3,BC=5,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F.
(1)求证:四边形CEDF是平行四边形;
(2)①当AE=时,四边 形CEDF是矩形;
形CEDF是矩形;
②当AE=时,四边形CEDF是菱形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com