练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】若（x2+3mx﹣）（x2﹣3x+n）的积中不含x和x3项，
    （1）求m2﹣mn+n2的值；
    （2）求代数式（﹣18m2n）2+（9mn）﹣2+（3m）2014n2016的值．

    【答案】解：（x2+3mx﹣）（x2﹣3x+n）=x4nx2+（3m﹣3）x3﹣9mx2+（3mn+1）x﹣x2﹣n，
    由积中不含x和x3项，得到3m﹣3=0，3mn+1=0，
    解得：m=1，n=﹣，
    （1）原式=（m﹣n）2=（）2=；
    （2）原式=324m4n2++（3mn）2014n2=36++=36．
    【解析】原式利用多项式乘以多项式法则计算，整理后根据积中不含x和x3项，求出m与n的值，
    （1）原式利用完全平方公式变形后，将m与n的值代入计算即可求出值；
    （2）原式利用幂的乘方与积的乘方，负整数指数幂法则变形，将各自的值代入计算即可求出值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】黄石农科所在相同条件下经试验发现蚕豆种子的发芽率为97.1%，请估计黄石地区1000斤蚕豆种子中不能发芽的大约有（　　）
    A.971斤
    B.129斤
    C.97.1斤
    D.29斤

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列统计量中，反映一组数据波动情况的是（　　）

    A. 平均数 B. 众数 C. 频率 D. 方差

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数学课上，我们知道可以用图形的面积来解释一些代数恒等式，如图1可以解释完全平方公式（a+b）2=a2+2ab+b2 ．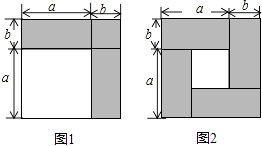
    （1）如图2，请用不同的代数式表示图中阴影部分的面积，由此，你能得到怎样的等式？
    （2）请说明这个等式成立；
    （3）已知（2m+n）2=13，（2m﹣n）2=5，请利用上述等式求mn．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个含有字母x，y的五次单项式，x的指数为3，且当x=2，y=-1时，这个单项式的值是32，求这个单项式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】能判断四边形是矩形的条件是( )

    A. 两条对角线互相平分 B. 两条对角线相等

    C. 两条对角线互相平分且相等 D. 两条对角线互相垂直

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知m，n是方程x2﹣2x﹣1＝0的两根，则（2m2﹣4m﹣1）（3n2﹣6n+2）的值等于_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】乘法公式的探究及应用．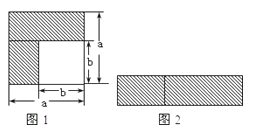

    （1）如图1，可以求出阴影部分的面积是 （写成两数平方差的形式）；
    （2）如图2，若将阴影部分裁剪下来，重新拼成一个矩形，它的宽是 ，长是 面积是 （写成多项式乘法的形式）；
    （3）比较图1、图2阴影部分的面积，可以得到公式 ；
    （4）运用你所得到的公式，计算下列各题：
    ①10.2×9.8，②（2m+n﹣p）（2m﹣n+p）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】因式分解：ax﹣ay=

    查看答案和解析>>

    同步练习册答案