
【题目】如图,四边形ABCD为矩形,连接AC,AD=2CD,点E在AD边上.
(1)如图1,若∠ECD=30°,CE=4,求△AEC的面积;
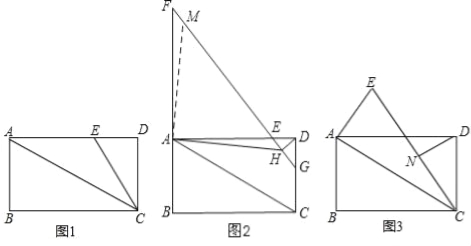
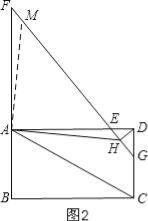
(2)如图2,延长BA至点F使得AF=2CD,连接FE并延长交CD于点G,过点D作DH⊥EG于点H,连接AH,求证:FH=![]() AH+DH;
AH+DH;
(3)如图3,将线段AE绕点A旋转一定的角度α(0°<α<360°)得到线段AE′,连接CE′,点N始终为CE′的中点,连接DN,已知CD=AE=4,直接写出DN的取值范围.
【答案】(1)12﹣2![]() ;(2)证明见解析(3)2
;(2)证明见解析(3)2![]() <DN≤2
<DN≤2![]()
【解析】
试题分析:(1)根据30°的直角三角形求CD和ED,再利用面积公式求△AEC的面积;
(2)作辅助线,构建全等三角形,证明△AFM≌△ADH,得AM=AH,FM=DH,则△MAH是等腰直角三角形,有MH=![]() AH,根据线段的和代入得结论;
AH,根据线段的和代入得结论;
(3)根据将线段AE绕点A旋转一定的角度α(0°<α<30°)得到线段AE′,先计算当AE旋转时DN的最小值和最大值,当α=0°时,DN最小;当α=180°时,DN最大,分别计算,写出结论.
试题解析:(1)在Rt△EDC中,∵∠EDC=30°,
∴ED=![]() EC=
EC=![]() ×4=2,cos30°=
×4=2,cos30°=![]() ,
,
∴DC=ECcos30°=4×![]() =2
=2![]() ,
,
∴AE=2DC﹣ED=4![]() ﹣2,
﹣2,
∴![]() =
=![]() ×AE×DC=
×AE×DC=![]() (4
(4![]() ﹣2)×2
﹣2)×2![]() =12﹣2
=12﹣2![]() ;
;
(2)过A作AM⊥AH,交FG于M,
∴∠MAH=∠MAD+∠DAH=90°,
又∵∠FAD=∠MAD+∠FAM=90°,
∴∠FAM=∠DAH,
∵AF∥CD,
∴∠F=∠FGD
∵DH⊥EG,
∴∠DHE=∠HDG+∠FGD=90°,
∠EDG=∠EDH+∠HDG=90°,
∴∠FGD=∠EDH,
∴∠F=∠EDH,
又∵AF=2CD,AD=2CD,
∴AF=AD,
∴△AFM≌△ADH,
∴AM=AH,FM=DH,
∴△MAH是等腰直角三角形,
∴MH=![]() AH,
AH,
∵FH=MH+FM,
∴FH=![]() AH+DH;
AH+DH;
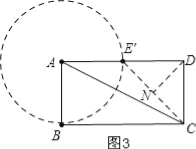
(3)∵线段AE绕点A旋转一定的角度α(0°<α<306°)得到线段AE′,
当α=0°时,点E′在AD中点,如图3,
∵四边形ABCD为矩形,CD=AE=4,AD=2CD,
∴∠CDE′=90°,DE′=CD=4,
∴△CDE′是等腰三角形,
又∵N是CE′的中点,
∴CE′⊥DN,
此时DN的值最小为2![]() ;
;
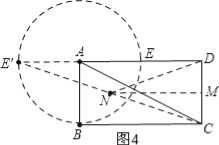
当α=180°时,E′在AD的延长线上,DN最长,
过N作CD垂线交CD于点M,
∵DE′=AE′+AD=12,CD=4,
∵MN⊥DC,DE′⊥DC,
∴MN∥DE′,
∴△CDE′∽△CMN,
∴![]() =
=![]() ,
,
∴MN=6,
则CM=DM=2,
∴在Rt△DMN中,DN=![]() =2
=2![]() ,
,
∵0°<α<360°
∴2![]() <DN≤2
<DN≤2![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】点A(x,y)为平面直角坐标系内一点,其中x,y满足3,x+2,y-4中的两个数相等,则所有的点A组成的图形为
A. 一个点B. 两条相交的直线C. 一个三角形D. 相交于一点的三条直线
查看答案和解析>>
科目:初中数学 来源: 题型:
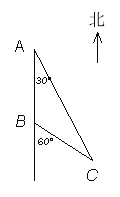
【题目】某地因持续高温干旱,村民饮水困难,镇政府组织村民组成水源行动小组到村镇周边找水。某村民在山洞![]() 里发现了暗河(如图所示),经勘察,在山洞的西面有一条南北走向的公路连接着
里发现了暗河(如图所示),经勘察,在山洞的西面有一条南北走向的公路连接着![]() 两村庄,山洞
两村庄,山洞![]() 位于
位于![]() 村庄南偏东
村庄南偏东![]() 方向,且位于
方向,且位于![]() 村庄南偏东
村庄南偏东![]() 方向。为方便
方向。为方便![]() 两村庄的村民取水,准备从山洞
两村庄的村民取水,准备从山洞![]() 处向公路
处向公路![]() 紧急修建一条最近的简易公路
紧急修建一条最近的简易公路![]() ,现已知
,现已知![]() 两村庄相距6千米。
两村庄相距6千米。
(1)求这条最近的简易公路![]() 的长(精确到0.1千米)?
的长(精确到0.1千米)?
(2)现由甲、乙两施工队共同合作修建这条公路,已知甲施工队修建2千米后,由乙施工队继续修建,乙施工队每天施工的速度是甲施工队每天施工速度的1.6倍,8天后,公路![]() 正式通车。求甲、乙两施工队每天修建公路多少千米?
正式通车。求甲、乙两施工队每天修建公路多少千米?
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解初三学生参加体育活动的情况,某校对部分初三学生进行了调查,其中一个问题是:“你平均每天参加体育活动的时间是多少?”共有4个选项:
A.1.5小时以上 B.1—1.5小时 C.0.5—1小时 D.0.5小时以下
根据调查结果绘制了两幅不完整的统计图如下:
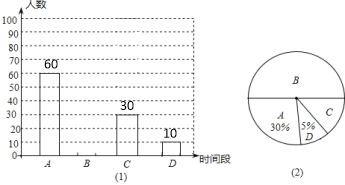
请你根据以上信息解答下列问题:
(1)本次调查的学生人数为 人,图(2)中选项C的圆心角度数为 度,请补全条形统计图。
(2)选择D选项的人中有2人来自一班,2人来自二班,学校准备从这4人中任选两人参加学校组织的师生趣味运动会,请你用列表法或画树状图的方法,求出所选的两人均来自同一个班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。 ![]()
(1)如图,已知点C在线段AB上,且AC=6cm,BC=4cm,M,N分别是AC,BC的中点,求线段MN的长度.
(2)在(1)中,如果AC=acm,BC=bcm,其他条件不变,求MN的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com