
【题目】综合题。 ![]()
(1)如图,已知点C在线段AB上,且AC=6cm,BC=4cm,M,N分别是AC,BC的中点,求线段MN的长度.
(2)在(1)中,如果AC=acm,BC=bcm,其他条件不变,求MN的长度.
【答案】
(1)解:因为M,N分别是AC,BC的中点所以,
MC= ![]() AC=
AC= ![]() ×6=3cm,
×6=3cm,
NC= ![]() BC=
BC= ![]() ×4=2cm,
×4=2cm,
所以,MN=MC+NC=3+2=5(cm)
(2)解:由(1)知MC= ![]() a,NC=
a,NC= ![]() b,
b,
所以,MN=MC+NC= ![]() a+
a+ ![]() b=
b= ![]() (a+b)
(a+b)
【解析】(1)根据线段中点的性质,可得MC、NC的长,根据线段的和差,可得答案;(2)根据线段中点的性质,可得MC、NC的长,根据线段的和差,可得答案.
【考点精析】关于本题考查的两点间的距离,需要了解同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记才能得出正确答案.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( ).
A.近似数3.76与3.760表示的意义一样
B.近似数13.2亿精确到亿位
C.3.0×103精确到百位,有4个有效数字
D.近似数30.000有5个有效数字
查看答案和解析>>
科目:初中数学 来源: 题型:
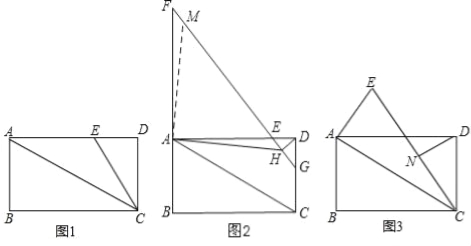
【题目】如图,四边形ABCD为矩形,连接AC,AD=2CD,点E在AD边上.
(1)如图1,若∠ECD=30°,CE=4,求△AEC的面积;
(2)如图2,延长BA至点F使得AF=2CD,连接FE并延长交CD于点G,过点D作DH⊥EG于点H,连接AH,求证:FH=![]() AH+DH;
AH+DH;
(3)如图3,将线段AE绕点A旋转一定的角度α(0°<α<360°)得到线段AE′,连接CE′,点N始终为CE′的中点,连接DN,已知CD=AE=4,直接写出DN的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学问题: 如图,在数轴上点A表示的数为﹣20,点B表示的数为40,动点P从点A出发以每秒5个单位长度的速度沿正方向运动,动点Q从原点出发以每秒4个单位长度的速度沿正方向运动,动点N从点B出发以每秒8个单位的速度先沿负方向运动,到达原点后立即按原速返回,三点同时出发,当点N回到点B时,三点停止运动.![]()
(1)三个动点运动t(0<t<5)秒时,则P、Q、N三点在数轴上所表示的三个数分别为 , , .
(2)当QN=10个单位长度时,求此时点P在数轴上所表示的数.
(3)尝试借助上面数学问题的解题经验,建立数轴完成下面实际问题: 码头C位于A、B两码头之间,且知AC=20海里,AB=60海里,甲船从A码头顺流驶向B码头,乙船从C码头顺流驶向B码头,丙船从B码头开往C码头后立即调头返回B码头.已知甲船在静水中航速为5海里/小时,乙船在静水中航速为4海里/小时,丙船在静水中航速为8海里/小时,水流速度为2海里/小时,三船同时出发,每艘船都行驶到B码头停止.
在整个运动过程中,是否存某一时刻,这三艘船中的一艘恰好在另外两船之间,且与两船的距离相等?若存在,请求出此时甲船离B码头的距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】浠水某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校初三学生的体重情况,从中随机抽取了80名初三学生的体重进行统计分析,在此问题中,样本是指( )
A. 80B. 被抽取的80名初三学生
C. 被抽取的80名初三学生的体重D. 该校初三学生的体重
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com