
����Ŀ���ˮij�̳�Ҫ��Ӫһ�������е��ľߣ�����Ϊ20Ԫ/������Ӫ���η��֣������۵�����25Ԫʱ��ÿ���������Ϊ250�������۵���ÿ����1Ԫ��ÿ����������ͼ���10����
(1)д���̳����������ľߣ�ÿ�����õ���������w(Ԫ)�����۵���x(Ԫ)֮��ĺ�����ϵʽ��
(2)�����۵���Ϊ����Ԫʱ�����ľ�ÿ��������������
(3)�̳���Ӫ���������������������A��B����Ӫ��������
����A�����ľߵ����۵��۸��ڽ����Ҳ�����30Ԫ��
����B��ÿ��������������10������ÿ���ľߵ���������Ϊ25Ԫ
��Ƚ����ַ��������������ߣ���˵�����ɣ�
���𰸡�(1)��w=��10![]() +700x��10000��(2)��35Ԫ��(3)��A���������.
+700x��10000��(2)��35Ԫ��(3)��A���������.
��������
���������(1)����������ó���������x�Ĺ�ϵ��Ȼ�����������=���������������ó���������ʽ��(2)�������κ���ת���ɶ���ʽ��Ȼ��ó���ֵ��(3)������A����ֵΪ��x=30ʱ������B��������ó�45��x��49��Ȼ����ݶ��κ����������Եó���ֵ.
���������(1)��������������=250-10��x-25��=-10x+500��
��w=��x-20����-10x+500��=-10x2+700x-10000��
(2)��w=-10x2+700x-10000=-10��x-35��2+2250��
��-10��0��������ͼ�����£�w�����ֵ��
��x=35ʱ��wmax=2250���ʵ�����Ϊ35Ԫʱ�����ľ�ÿ����������
(3)��A��������ߣ��������£�
A�����У�20��x��30���ʵ�x=30ʱ��w�����ֵ�� ��ʱwA=2000��
B�����У� 10x+500��10��x-20��25 ��x��ȡֵ��ΧΪ��45��x��49��
������w=-10��x-35��2+2250���Գ���Ϊx=35������x=45ʱ��w�����ֵ����ʱwB=1250��
��wA��wB����A����������ߣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y��![]() (mΪ��������m��5)��
(m��������m��5)��
(1)������ͼ���ÿ����֧�ϣ�y��x�������������m��ȡֵ��Χ��
(2)����ͼ����һ�κ���y����x��1��ͼ���һ���������������3����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1��a3��a2b+ab2+a2b��ab2+b2
��2��3��2x2��y2����2��3y2��2x2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽����ѧ���μ�������������ijУ�Բ��ֳ���ѧ�������˵��飬����һ�������ǣ�����ƽ��ÿ��μ��������ʱ���Ƕ��٣�������4��ѡ�
A.1.5Сʱ���� B.1��1.5Сʱ C.0.5��1Сʱ D.0.5Сʱ����
���ݵ�����������������������ͳ��ͼ���£�
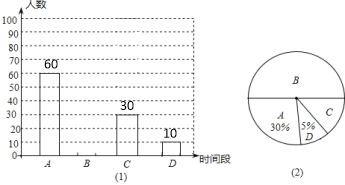
�������������Ϣ����������⣺
��1�����ε����ѧ������Ϊ �ˣ�ͼ��2����ѡ��C��Բ�ĽǶ���Ϊ �ȣ��벹ȫ����ͳ��ͼ��
��2��ѡ��Dѡ���������2������һ�࣬2�����Զ��࣬ѧУ������4������ѡ���˲μ�ѧУ��֯��ʦ��Ȥζ�˶��ᣬ�������б�������״ͼ�ķ����������ѡ�����˾�����ͬһ����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ��⡣ ![]()
��1����ͼ����֪��C���߶�AB�ϣ���AC=6cm��BC=4cm��M��N�ֱ���AC��BC���е㣬���߶�MN�ij��ȣ�
��2���ڣ�1���У����AC=acm��BC=bcm�������������䣬��MN�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ɫ����ɫũ��Ʒ�ڹ����г����ľ߾������������㹽Զ���ձ��ͺ����ȵأ�����ʱ������������г��۸�10Ԫ/ǧ���������չ���2000ǧ���㹽���������У���Ԥ�⣬�㹽���г��۸�ÿ��ÿǧ�˽�����0.5Ԫ��������������㹽ʱÿ����Ҫ֧�����ַ��úϼ�340Ԫ�������㹽���������ౣ��110�죬ͬʱ��ƽ��ÿ����6ǧ�˵��㹽���ܳ��ۣ�
��1�������![]() ��������㹽һ���Գ��ۣ��������㹽�������ܽ��Ϊ
��������㹽һ���Գ��ۣ��������㹽�������ܽ��Ϊ![]() Ԫ����д��
Ԫ����д��![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2�������������22500Ԫ���轫�����㹽��Ŷ��������ۣ������������ܽ��չ��ɱ������ַ��ã�
��3������������㹽��Ŷ��������ۿɻ�����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���Ǻ����IJ��ǵĶ���֮����1��5��������ǵĶ����ǣ�������
A. 10�� B. 30�� C. 60�� D. 80��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������ӳ��г�����������2km������С�ռң�����������3km����С��ң�����������9km����СӢ�ң����ص����У�
��1�����Գ���Ϊԭ�㣬������Ϊ��������1����λ���ȱ�ʾ1km���������ᣮ���������ϱ�ʾ��С�ռҡ�С��ҡ�СӢ�ҵ�λ�ã�
��2��СӢ�Ҿ�С�ռ��ж�Զ��
��3������һ����ʻ�˶���ǧ�ף�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com