
早晨小欣与妈妈同时从家里出发,步行与骑自行车到方向相反的两地上学与上班,图是他们离家的路程 y (米)与时间 x (分)的函数图象.妈妈骑车走了10分时接到小欣的电话,即以原速骑车前往小欣学校,并与小欣同时到达学校.已知小欣步行速度为每分50米,
求小欣家与学校距离及小欣早晨上学需要的时间.

解:方法一:
由图象知,妈妈骑车的速度为2500÷10=250(米/分)。
设小欣家与学校距离为y米,
根据题意,得![]()
解得![]()
![]()
答:小欣家与学校距离为1250米,小欣早晨上学需要的时间为25分
方法二:
由图象知,妈妈骑车的速度为2500÷10=250(米/分)。
设小欣上学需要步行x分,
根据题意,得![]()
解得x=25
![]()
答:小欣家与学校距离为1250米,小欣早晨上学需要的时间为25分
方法三:
设直线OB的解析式为![]()
![]() 当
当![]() =10时,10×50=500,
=10时,10×50=500,
![]() 直线OB经过点(10,500),…………………………………………………1分
直线OB经过点(10,500),…………………………………………………1分
![]() 500=10
500=10![]() ,解得
,解得![]() =50。
=50。![]() 直线OB的解析式为
直线OB的解析式为![]() …………………2分
…………………2分
设直线AB的解析式为![]() ,
,
由题意知,C点坐标为(20,0)
![]() 直线AB经过点A(10,-2500)、C(20,0)
直线AB经过点A(10,-2500)、C(20,0)
![]()
解得![]()
![]()
![]()
解方程组![]()
解得![]()
答:小欣家与学校距离为1250米,小欣早晨上学需要的时间为25分
方法四:
由图象知,妈妈骑车的速度为2500÷10=250(米/分)。
设妈妈骑车赶往小欣学校需要x分,则小欣步行上学需要(x+10)分
根据题意,得![]()
解得x=15。
![]()
答:小欣家与学校距离为1250米,小欣早晨上学需要的时间为25分
方法五:
 如图,过点B作BD
如图,过点B作BD![]()
![]() 轴,垂足为D,过点A作AE
轴,垂足为D,过点A作AE![]()
![]() 轴,垂足为E,则BD为小欣家与学校的距离,OD为小欣步行上学需要的时间。
轴,垂足为E,则BD为小欣家与学校的距离,OD为小欣步行上学需要的时间。
由题意知,
![]()
![]()
由题意知,OE=EC=10,AE![]() OC,
OC,![]() OA=AC.
OA=AC.![]()
![]() AOC=
AOC=![]() ACO.
ACO.
![]()
![]() ACO=
ACO=![]() BCD,
BCD,![]()
![]() BCD=
BCD=![]() AOC
AOC
![]()
![]()
![]()
![]()
![]()
![]()
答:小欣家与学校距离为1250米,小欣早晨上学需要的时间为25分
方法六:
如图,过点B作BD![]()
![]() 轴,垂足为D,过点A作AE
轴,垂足为D,过点A作AE![]()
![]() 轴,垂足为E,AE的延长线交OB于F,则BD为小欣家与学校的距离,OD为小欣步行上学需要的时间。
轴,垂足为E,AE的延长线交OB于F,则BD为小欣家与学校的距离,OD为小欣步行上学需要的时间。
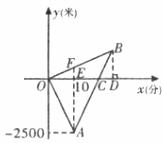
由题意知,OE=EC=10,EF=50×10=500。
![]() AF
AF![]()
![]() 轴,BD
轴,BD![]()
![]() 轴,
轴,![]()
![]()
又 ![]()
![]()
![]() BD=1250
BD=1250
![]() CD=5,
CD=5,![]() OD=OC+CD=OE+EC+CD=10+10+5=25
OD=OC+CD=OE+EC+CD=10+10+5=25
答:小欣家与学校距离为1250米,小欣早晨上学需要的时间为25分


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
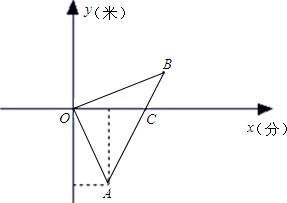 间x (分)的函数图象如图所示.已知A点坐标A(10,-2500),C(20,0)C点坐标为(20,0).
间x (分)的函数图象如图所示.已知A点坐标A(10,-2500),C(20,0)C点坐标为(20,0).查看答案和解析>>
科目:初中数学 来源: 题型:
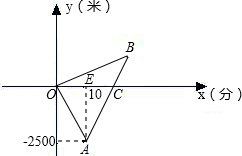 校.已知小欣步行速度为每分50米,求小欣家与学校距离及小欣早晨上学需要的时间.
校.已知小欣步行速度为每分50米,求小欣家与学校距离及小欣早晨上学需要的时间.查看答案和解析>>
科目:初中数学 来源: 题型:
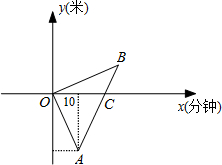 学校,完成下列问题:
学校,完成下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 时接到小欣的电话,立即以原来的速度返回并前往学校,若已知小欣步行的速度为50米/分钟,并且妈妈与小欣同时到达学校.完成下列问题:
时接到小欣的电话,立即以原来的速度返回并前往学校,若已知小欣步行的速度为50米/分钟,并且妈妈与小欣同时到达学校.完成下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com