C
分析:首先过点A作AD⊥BC于D,由等腰三角形的性质,可得BD=CD=

BC=1,∠B=∠C,由勾股定理可求得AD的长,又可证得△BN
1P
1∽△BAD,利用相似三角形的对应边成比例,可证得N
1P
1=2BP
1,又由△BP
1N
1≌△CQ
1M
1(AAS),BP
1=CQ
1,则可求得c
1的值,同理可求得c
2,c
3的值,继而求得答案.
解答:
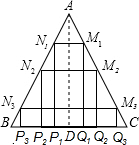
解:过点A作AD⊥BC于D,
∵AB=AC=

,BC=2,
∴BD=CD=

BC=1,∠B=∠C,
∴AD=

=2,
∵四边形P
1Q
1M
1N
1是矩形,
∴P
1Q
1=M
1N
1,N
1P
1=M
1Q
1,N
1P
1⊥BC,
∴N
1P
1∥AD,
∴△BN
1P
1∽△BAD,
∴BP
1:BD=N
1P
1:AD,
∴N
1P
1=2BP
1,
在△BP
1N
1和△CQ
1M
1中,
∵
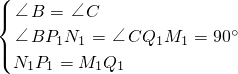
,
∴△BP
1N
1≌△CQ
1M
1(AAS),
∴BP
1=CQ
1,
∴c
1=N
1P
1+P
1Q
1+M
1Q
1+M
1N
1=2BP
1+2P
1Q
1+2BP
1=2(BP
1+P
1Q
1+BP
1)=2(BP
1+P
1Q
1+CQ
1)=2BC=2×2=4,
同理:c
2=c
3=c
1=4.
∴c
1+c
2+c
3=12.
故选C.
点评:此题考查了相似三角形的判定与性质、矩形的性质、等腰三角形的性质、全等三角形的判定与性质以及勾股定理.此题难度较大,注意掌握辅助线的作法,注意数形结合思想与整体思想的应用.

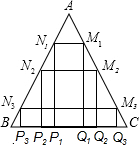 如图,在△ABC中,AB=AC=
如图,在△ABC中,AB=AC= ,BC=2.现分别任作△ABC的内接矩形P1Q1M1N1,P2Q2M2N2,P3Q3M3N3,设这三个内接矩形的周长分别为c1、c2,c3,则c1+c2+c3的值是
,BC=2.现分别任作△ABC的内接矩形P1Q1M1N1,P2Q2M2N2,P3Q3M3N3,设这三个内接矩形的周长分别为c1、c2,c3,则c1+c2+c3的值是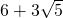
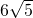
 BC=1,∠B=∠C,由勾股定理可求得AD的长,又可证得△BN1P1∽△BAD,利用相似三角形的对应边成比例,可证得N1P1=2BP1,又由△BP1N1≌△CQ1M1(AAS),BP1=CQ1,则可求得c1的值,同理可求得c2,c3的值,继而求得答案.
BC=1,∠B=∠C,由勾股定理可求得AD的长,又可证得△BN1P1∽△BAD,利用相似三角形的对应边成比例,可证得N1P1=2BP1,又由△BP1N1≌△CQ1M1(AAS),BP1=CQ1,则可求得c1的值,同理可求得c2,c3的值,继而求得答案. 解:过点A作AD⊥BC于D,
解:过点A作AD⊥BC于D, ,BC=2,
,BC=2, BC=1,∠B=∠C,
BC=1,∠B=∠C, =2,
=2,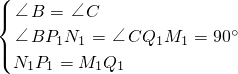 ,
,

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为