
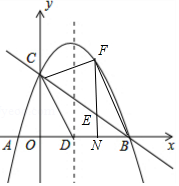
 ��ͼ��������y=-$\frac{1}{2}$x2+mx+n��x�ύ��A��B���㣬��y�ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D����֪A��-1��0����C��0��2����
��ͼ��������y=-$\frac{1}{2}$x2+mx+n��x�ύ��A��B���㣬��y�ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D����֪A��-1��0����C��0��2�������� ��1�����ô���ϵ����������κ�������ʽ���ɣ�
��2�����������ߵĽ���ʽ���B������꣬Ȼ����ݴ���ϵ�������ֱ��BC�Ľ���ʽ���������E�����꣬��ɱ�ʾ����F�����꣬������ʾ��EF�ij��ȣ���ɱ�ʾ����CBF��������Ӷ��ɱ�ʾ���ı���CDBF����������ö��κ��������ʣ�����������ֵ����ʱE������ꣻ
��3�������P�����꣬�Ӷ��ɱ�ʾ��PC��PD�ij����������ɵ�PC=CD��PD=CD���ɵõ�����P������ķ��̣�����õ�P�����꣮
���  �⣺
�⣺
��1��������y=-$\frac{1}{2}$x2+mx+n��x�ύ��A��B���㣬��y�ύ�ڵ�C��A��-1��0����C��0��2����
��$\left\{\begin{array}{l}{-\frac{1}{2}-m+n=0}\\{n=2}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{m=\frac{3}{2}}\\{n=2}\end{array}\right.$��
�������߽���ʽΪy=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2��
��2����y=0����-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=0�����x1=-1��x2=4��
��B��4��0����
��ֱ��BC�Ľ���ʽΪy=kx+b��
��$\left\{\begin{array}{l}{4k+b=0}\\{b=2}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$��
��ֱ��BC�Ľ���ʽΪy=-$\frac{1}{2}$x+2��
��E��m��-$\frac{1}{2}$m+2������F��m��-$\frac{1}{2}$m2+$\frac{3}{2}$m+2����
��EF=��-$\frac{1}{2}$m2+$\frac{3}{2}$m+2��-��-$\frac{1}{2}$m+2��=-$\frac{1}{2}$m2+2m=-$\frac{1}{2}$��m-2�� 2+2��
��S��BFC=$\frac{1}{2}$EF��4=2EF=-��m-2��2+4=-m2+4m��
��y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=-$\frac{1}{2}$��x-$\frac{3}{2}$��2+$\frac{25}{8}$��
��D��$\frac{3}{2}$��0����
��BD=4-$\frac{3}{2}$=$\frac{5}{2}$��
��S��BCD=$\frac{1}{2}$BD•OC=$\frac{1}{2}$��$\frac{5}{2}$��2=$\frac{5}{2}$��
��S�ı���CDBF=S��BFC+S��BCD=-m2+4m+$\frac{5}{2}$=-��m-2��2+$\frac{13}{2}$��
��-1��0��
�൱m=2ʱ��S�ı���CDBF�����ֵ�����ֵΪ$\frac{13}{2}$����ʱE������Ϊ��2��1����
��3�����������P��������$\frac{3}{2}$��t����
��D��$\frac{3}{2}$��0����C��0��2����
��CD=$\sqrt{��\frac{3}{2}��^{2}+{2}^{2}}$=$\frac{5}{2}$��PD=|t|��PC=$\sqrt{��\frac{3}{2}��^{2}+��t-2��^{2}}$��
�ߡ�PCD����CDΪ���ĵ��������Σ�
����PD=CD��PC=CD��
�ٵ�PD=CDʱ������|t|=$\frac{5}{2}$�����t=��$\frac{5}{2}$����ʱP������Ϊ��$\frac{3}{2}$��$\frac{5}{2}$����$\frac{3}{2}$��-$\frac{5}{2}$����
�ڵ�PC=CDʱ������$\frac{5}{2}$=$\sqrt{��\frac{3}{2}��^{2}+��t-2��^{2}}$�����t=0��t=4����t=0ʱ����P���D�غϣ���ȥ��
��t=4����ʱ��P����Ϊ��$\frac{3}{2}$��4����
���Ͽ�֪�������������ĵ�P��������Ϊ��$\frac{3}{2}$��$\frac{5}{2}$����$\frac{3}{2}$��-$\frac{5}{2}$����$\frac{3}{2}$��4����
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰����ϵ�����������ε���������κ��������ʡ����������ε����ʡ�����˼�뼰��������˼���֪ʶ���ڣ�1����ע�����ϵ������Ӧ�ã��ڣ�2������E�������ʾ���ı���CDBF������ǽ���Ĺؼ����ڣ�3������P�������ʾ��PD��PC�ij��ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�


 ������ϰ�ο����뵥Ԫ���ϵ�д�
������ϰ�ο����뵥Ԫ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���� | B�� | Բ�� | C�� | Բ | D�� | ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
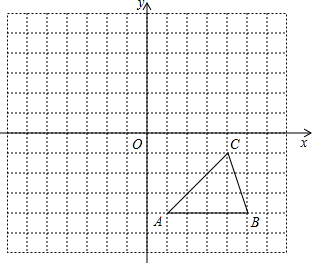 ��ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��ڽ���ƽ��ֱ������ϵ��ABC�Ķ�����ڸ���ϣ���C������Ϊ��4��-1����
��ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��ڽ���ƽ��ֱ������ϵ��ABC�Ķ�����ڸ���ϣ���C������Ϊ��4��-1�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� | 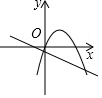 | C�� | 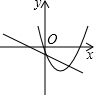 | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
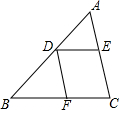 ��ͼ���ڡ�ABC�У�D��AB����һ�㣬DE��BC��DF��AC�����н�����ȷ���ǣ�������
��ͼ���ڡ�ABC�У�D��AB����һ�㣬DE��BC��DF��AC�����н�����ȷ���ǣ�������| A�� | $\frac{AD}{BD}$=$\frac{AE}{AC}$ | B�� | $\frac{DE}{BF}$=$\frac{AE}{AC}$ | C�� | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | D�� | $\frac{AD}{BD}$=$\frac{DF}{AC}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com