
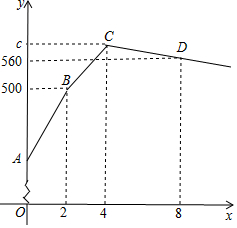
 某手工编织厂生产一种旅游纪念品,现有60名工人进行手工编织(每人编织的效率相同),2天后抽出10名工人执行其他任务,其余工人继续编织生产;2天后从编织的工人中再抽出10名进行销售(每人每天的销售量相同).已知每人每天的销售量是编织量的5倍,下图是产品库存量y(件)与生产时间x(天)之间的函数关系图象.
某手工编织厂生产一种旅游纪念品,现有60名工人进行手工编织(每人编织的效率相同),2天后抽出10名工人执行其他任务,其余工人继续编织生产;2天后从编织的工人中再抽出10名进行销售(每人每天的销售量相同).已知每人每天的销售量是编织量的5倍,下图是产品库存量y(件)与生产时间x(天)之间的函数关系图象.分析 (1)根据题意和函数图象可以得到点B的实际意义;
(2)根据题意和函数图象中的数据可以求得每人每天的编织量和销售量;
(3)根据(2)中的答案可以求得点C的坐标,从而可以求得CD段所在的直线的函数表达式,由(2)中的答案可以求得原来的库存量,从而可以求得多少天后剩余库存量低于生产前的库存量.
解答 解:(1)点B的实际意义是60名工人2天生产的纪念品数量与库存量之和是500件;
(2)设每人每天的编织量是x件,
500+(60-10)x×(4-2)+(60-10-10)x×(8-4)-(8-4)×5x×10=560,
解得,x=1,
∴5x=5
即每人每天的编织量是1件,销售量是5件;
(3)由(2)可得,
点C的纵坐标的值是:500+(60-10)×1×2=600,
即点C的坐标为(4,600),
又∵点D(8,560),
设CD段所在的直线的函数表达式为y=kx+b,
$\left\{\begin{array}{l}{4k+b=600}\\{8k+b=560}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=-10}\\{b=640}\end{array}\right.$,
即CD段所在的直线的函数表达式是y=-10x+640,
由题意可得,原来的库存量为:500-60×1×2=380,
则-10x+640<380,
解得,x>26,
即26天后剩余库存量低于生产前的库存量.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,会用待定系数求函数的解析式,注意数形结合的思想的灵活运用.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:解答题
 请将下列说理过程补充完整:
请将下列说理过程补充完整:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 品牌 | 进价(无/件) | 售价(元/件) |
| A | 50 | 80 |
| B | 40 | 65 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{5}{4}$ | B. | $\frac{5}{4}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
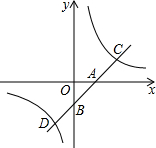 如图所示,直线y=kx+b分别交x轴、y轴于点A(1,0),B(0,-1),交双曲线y=$\frac{m}{x}$于点C,D,且AB=AC.
如图所示,直线y=kx+b分别交x轴、y轴于点A(1,0),B(0,-1),交双曲线y=$\frac{m}{x}$于点C,D,且AB=AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com