
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm. 
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与面积.
【答案】
(1)证明:证明:∵四边形EFGH是正方形,
∴EH∥BC,
∴∠AEH=∠B,∠AHE=∠C,
∴△AEH∽△ABC
(2)解:如图 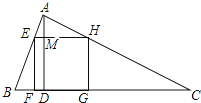 设AD与EH交于点M.
设AD与EH交于点M.
∵∠EFD=∠FEM=∠FDM=90°,
∴四边形EFDM是矩形,
∴EF=DM,设正方形EFGH的边长为x,
∵△AEH∽△ABC,
∴ ![]() ,
,
∴ ![]() ,
,
∴x= ![]() ,
,
∴正方形EFGH的边长为 ![]() cm,面积为
cm,面积为 ![]() cm2
cm2
【解析】(1)根据EH∥BC即可证明.(2)如图设AD与EH交于点M,首先证明四边形EFDM是矩形,设正方形边长为x,再利用△AEH∽△ABC,得 ![]() =
= ![]() ,列出方程即可解决问题.本题考查正方形的性质、相似三角形的判定和性质等知识,解题的关键是利用相似三角形的相似比对于高的比,学会用方程的思想解决问题,属于中考常考题型.
,列出方程即可解决问题.本题考查正方形的性质、相似三角形的判定和性质等知识,解题的关键是利用相似三角形的相似比对于高的比,学会用方程的思想解决问题,属于中考常考题型.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D在⊙O上,∠A=2∠BCD,点E在AB的延长线上,∠AED=∠ABC 
(1)求证:DE与⊙O相切;
(2)若BF=2,DF= ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下: 如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD.垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.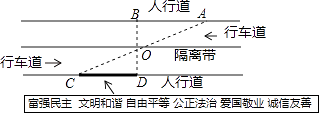
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的两格中,点A、B、C都是格点.
(1)将△ABC向左平移6个单位长度得到得到△A1B1C1;
(2)将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2 , 请画出△A2B2C2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上一点,AD垂直于过点C的切线,垂足为D. 
(1)求证:AC平分∠BAD;
(2)若AC=2 ![]() ,CD=2,求⊙O的直径.
,CD=2,求⊙O的直径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com