
【题目】如图,AB是⊙O的直径,C是⊙O上一点,AD垂直于过点C的切线,垂足为D. 
(1)求证:AC平分∠BAD;
(2)若AC=2 ![]() ,CD=2,求⊙O的直径.
,CD=2,求⊙O的直径.
【答案】
(1)证明:如图,连接OC,
∵DC切⊙O于C,
∴OC⊥CF,
∴∠ADC=∠OCF=90°,
∴AD∥OC,
∴∠DAC=∠OCA,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠DAC=∠OAC,即AC平分∠BAD

(2)解:连接BC.
∵AB是直径,
∴∠ACB=90°=∠ADC,
∵∠DAC=∠BAC,
∴△ADC∽△ACB,
∴ ![]() ,
,
在Rt△ADC中,AC=2 ![]() ,CD=2,
,CD=2,
∴AD=4,
∴ ![]() ,
,
∴AB=5.

【解析】(1)连接OC,根据切线的性质判断出AD∥OC,得到∠DAC=∠OCA,再根据OA=OC得到∠OAC=∠OCA,可得AC平分∠BAD.(2)连接BC,得到△ADC∽△ACB,根据相似三角形的性质即可求出AB的长.
【考点精析】根据题目的已知条件,利用角平分线的性质定理和勾股定理的概念的相关知识可以得到问题的答案,需要掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm. 
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠B=60°,∠FAC、∠ECA是△ABC的两个外角,AD平分∠FAC,CD平分∠ECA. 求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A(0,2),直线OP位于一、三象限,∠AOP=45°(如图1),设点A关于直线OP的对称点为B.
(1)写出点B的坐标;
(2)过原点O的直线l从OP的位置开始,绕原点O顺时针旋转. ①如图1,当直线l顺时针旋转10°到l1的位置时,点A关于直线l1的对称点为C,则∠BOC的度数是 , 线段OC的长为;
②如图2,当直线l顺时针旋转55°到l2的位置时,点A关于直线l2的对称点为D,则∠BOD的度数是;
③直线l顺时针旋转n°(0<n≤90),在这个运动过程中,点A关于直线l的对称点所经过的路径长为(用含n的代数式表示).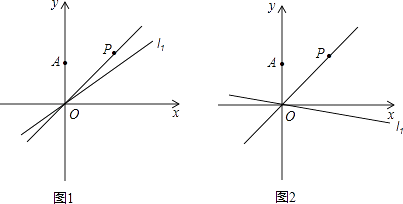
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是边AB、AC的中点,∠B=50°.先将△ADE沿DE折叠,点A落在三角形所在平面内的点为A1 , 则∠BDA1的度数为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识迁移 当a>0且x>0时,因为 ![]() ,所以x﹣
,所以x﹣ ![]() +
+ ![]() ≥0,从而x+
≥0,从而x+ ![]() ≥
≥ ![]() (当x=
(当x= ![]() )是取等号).
)是取等号).
记函数y=x+ ![]() (a>0,x>0).由上述结论可知:当x=
(a>0,x>0).由上述结论可知:当x= ![]() 时,该函数有最小值为2
时,该函数有最小值为2 ![]() .
.
直接应用
已知函数y1=x(x>0)与函数y2= ![]() (x>0),则当x=1时,y1+y2取得最小值为2.
(x>0),则当x=1时,y1+y2取得最小值为2.
变形应用
已知函数y1=x+1(x>﹣1)与函数y2=(x+1)2+4(x>﹣1),求 ![]() 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值.
实际应用
已知某汽车的一次运输成本包含以下三个部分,一是固定费用,共360元;二是燃油费,每千米1.6元;三是折旧费,它与路程的平方成正比,比例系数为0.001.设该汽车一次运输的路程为x千米,求当x为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,小刚一家乘车去离家380公里的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.
(1)从小刚家到该景区乘车一共用了多少时间?
(2)求线段AB对应的函数解析式;
(3)小刚一家出发2.5小时时离目的地多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小军同学在学校组织的社会实践活动中,负责了解他所居住的小区450户具名的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表:
月均用水量 | 2≤x<3 | 3≤x<4 | 4≤x<5 | 5≤x<6 | 6≤x<7 | 7≤x<8 | 8≤x<9 |
频数 | 2 | 12 | ① | 10 | ② | 3 | 2 |
百分比 | 4% | 24% | 30% | 20% | ③ | 6% | 4% |
(1)请根据题中已有的信息补全频数分布: , , ;
(2)如果家庭月均用水量在5≤x<8范围内为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?
(3)记月均用水量在2≤x<3范围内的两户为a1 , a2 , 在7≤x<8范围内的3户b1、b2、b3 , 从这5户家庭中任意抽取2户,试完成下表,并求出抽取出的2户家庭来自不同范围的概率.
a1 | a2 | b1 | b2 | b3 | |
a1 | |||||
a2 | |||||
b1 | |||||
b2 | |||||
b3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com