
【题目】如图,在等边△ABC中,M是AC上一点,N是BC上一点,且AM=BN,∠MBC=25°,AN与BM交于点O,则∠MON的度数为( )
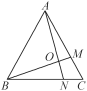
A. 110° B. 105° C. 90° D. 85°
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿AB边向点B以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动;如果同时出发,则过3秒时,求△BPQ的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DEF都是等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,射线EF与线段AB相交于点G,与射线CA相交于点Q.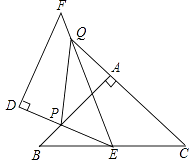
(1)求证:△BPE∽△CEQ;
(2)求证:DP平分∠BPQ;
(3)当BP=a,CQ= ![]() a,求PQ长(用含a的代数式表示).
a,求PQ长(用含a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线距离之和PE+PF是( )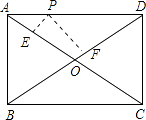
A.4.8
B.5
C.6
D.7.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学的1号教学大楼共有4道门,其中两道正门大小相同,两道侧门也大小相同,安全检查时,对4道门进行了测试,当同时开启一道正门和两道侧门时,2分钟内可以通过560名学生,当同时开启一道正门和一道侧门时,4分钟内可通过800名学生.
(1)求平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)该中学的2号教学大楼,有和1号教学大楼相同的正门和侧门共5道,若这栋大楼的教室里最多有1920名学生,安全检查规定,在紧急情况下,全大楼学生应在4分钟内通过这5道门安全撤离,该栋大楼正门和侧门各有几道?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,E是AB延长线上一点,F是DC延长线上一点,连接BF,EF,恰有BF=EF,将线段EF绕点F顺时针旋转90°得FG,过点B作EF的垂线,交EF于点M,交DA的延长线于点N,连接NG.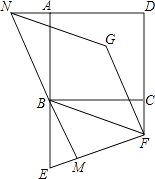
(1)求证:BE=2CF;
(2)试猜想四边形BFGN是什么特殊的四边形,并对你的猜想加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张两边分别平行的纸条折成如图所示,EF为折痕,ED交BF于点G,且∠EFB=48°,则下列结论: ①∠DEF=48°;②∠AED=84°;③∠BFC=84°;④∠DGF=96°,其中正确的个数有( )
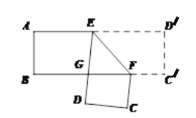
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副直角三角板如图放置,使GM与AB在同一直线上,其中点M在AB的中点处,MN与AC交于点E,∠BAC=30°,若AC=9cm,则EM的长为( )
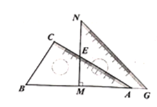
A. 2.5cm B. 3cm C. 4cm D. 4.5cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com