Question

10．如图，正方形ABCD中，E、F分别在BC、CD上，且AE=BE+DF
（1）求证：∠DAE=2∠DAF；
（2）过D作DH⊥AF于H，连接CH，且∠CHF=45°，探究FH与AE的数量关系，并证明．

Answer 1

分析 （1）延长CB到K，使BK=DF，连接AG，易证△ADF≌△ABK，根据AE=EB+DF=EB+KB=EK，所以∠K=∠KAE=∠AFD=∠BAF，故∠DAF=∠EAF．
（2）如图2，延长DH交AE于K，连接KC．作CM⊥AF交AF的延长线于M，连接DM，CM，AC，FK，EF，先证明四边形DMCH是平行四边形，四边形CMHK是正方形，设HF=a，求出AE即可解决AE与HF的关系．

解答 （1）证明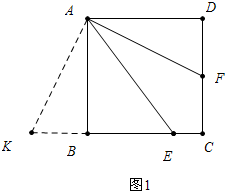：延长CB到K，使BK=DF，连接AG，
∵四边形ABCD是正方形，
∴AB=AD，∠ADF=∠ABE=∠ABK=90°，AB∥DC，
在△ABK和△ADF中，
$\left\{\begin{array}{l}{AD=AB}\\{∠ADF=∠ABK}\\{DF=BK}\end{array}\right.$，
∴△ADF≌△ABK，
∴∠AFD=∠K=∠BAF，∠BAK=∠DAF，
∵AE=BE+DF，BK=DF，
∴AE=KE，
∴∠K=∠EAK=∠BAF，
∴∠BAK=∠EAF，
∴∠DAF=∠EAF，
∴∠DAE=2∠DAF．
（2）结论：$\frac{AE}{HF}=\frac{5\sqrt{5}}{2}$，利用如下：
如图2，延长DH交AE于K，连接KC．作CM⊥AF交AF的延长线于M，连接DM，CM，AC，FK，EF，
∵∠DAH=∠KAH，∠DAH+∠ADH=90°，∠KAH+∠AKH=90°，
∴∠ADH=∠AKH，
∴AD=AK，
∵AH⊥DK，∴DH=HK，FD=FK
∵∠ADF=∠FMC=90°，∠AFD=∠CFM，
∴△AFD∽△CFM，
∴$\frac{AF}{CF}=\frac{DF}{FM}$，
∴$\frac{AF}{DF}=\frac{CF}{FM}$，∵∠AFC=∠DFM，
∴△AFC∽△DFM，
∴∠DMF=∠ACF=45°，
∵∠CHM=45°，
∴∠DMH=∠CHM，
∴CH∥DM，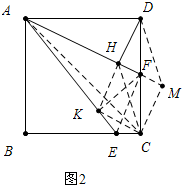
∵DH⊥AM，CM⊥AM，
∴DK∥MC，
∴四边形DHCM是平行四边形，
∴DF=FC=FK，
∴∠DKC=90°，
∵∠HKC=∠KHM=∠HMC=90°，
∴四边形HKCM是矩形，
∵MH=MC，
∴四边形HKCM是正方形，
设HF=a，则DH=HK=KC=2a，AD=CD=AK=2$\sqrt{5}$a，FK=DF=FC=$\sqrt{5}$a，
∵FK=FC，FK⊥KE，FC⊥CE，
∴∠KEF=∠CEF，∠KFE=∠CFE=∠KDF=∠FKD，
∴△DHF∽△FKE，
∴$\frac{DH}{FK}=\frac{HF}{EK}$，
∴$\frac{2a}{\sqrt{5}a}=\frac{a}{EK}$，
∴EK=$\frac{\sqrt{5}}{2}$a，AK=$\frac{5\sqrt{5}}{2}$a，
∴$\frac{AE}{HF}=\frac{\frac{5\sqrt{5}}{2}a}{a}$=$\frac{5\sqrt{5}}{2}$．

点评 本题考查了正方形的性质、全等三角形的判定和性质、平行四边形的判定和性质、正方形的判定和性质等知识，学会添加辅助线构造平行四边形、正方形解决问题．