
【题目】如图,以正方形![]() 的顶点
的顶点![]() 为坐标原点,直线
为坐标原点,直线![]() 为
为![]() 轴建立直角坐标系,对角线
轴建立直角坐标系,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 为
为![]() 上一点,点
上一点,点![]() 坐标为
坐标为![]() ,则点
,则点![]() 绕点
绕点![]() 顺时针旋转90°得到的对应点
顺时针旋转90°得到的对应点![]() 的坐标是( )
的坐标是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
如图,连接PE,点P绕点E顺时针旋转90°得到的对应点P′在x轴上,根据正方形的性质得到∠ABC=90°,∠AEB=90°,AE=BE,∠EAP′=∠EBP=45°,由点P坐标为(a,b),得到BP=b,根据全等三角形的性质即可得到结论.
如图,连接PE,点P绕点E顺时针旋转90°得到的对应点P′在x轴上,
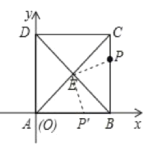
∵四边形ABCD 是正方形,
∴∠ABC=90°,
∴∠AEB=90°,AE=BE,∠EAP′=∠EBP=45°,
∵点P坐标为(a,b),
∴BP=b,
∵∠PEP′=90°,
∴∠AEP′=∠PEB,
在△AEP′与△BEP中,
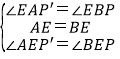 ,
,
∴△AEP′≌△BEP(ASA),
∴AP′=BP=b,
∴点P′的坐标是(b,0),
故选:D.


科目:初中数学 来源: 题型:
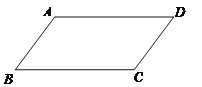
【题目】如图,已知AD∥BC,要使四边形ABCD为平行四边形,需要增加的一个条是:_____.(只填一个你认为正确的条件即可,不添加任何线段与字母)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数的图象经过三个点A(﹣4,﹣3),B(2m,y1),C(6m,y2),其中m>0.
(1)当y1﹣y2=4时,求m的值;
(2)如图,过点B、C分别作x轴、y轴的垂线,两垂线相交于点D,点P在x轴上,若三角形PBD的面积是8,请写出点P坐标(不需要写解答过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在四边形ABCD中,∠A=∠C=90°.
(1)∠ABC+∠ADC= °;
(2)如图①,若DE平分∠ADC,BF平分∠ABC的外角,请写出DE与BF的位置关系,并证明;
(3)如图②,若BE,DE分别四等分∠ABC、∠ADC的外角(即∠CDE=![]() ∠CDN,∠CBE=
∠CDN,∠CBE=![]() ∠CBM),试求∠E的度数.
∠CBM),试求∠E的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“宏扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“A﹣国学诵读”、“B﹣演讲”、“C﹣课本剧”、“D﹣书法”,要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如下:
(1)如图,希望参加活动C占20%,希望参加活动B占15%,则被调查的总人数为 人,扇形统计图中,希望参加活动D所占圆心角为 度,根据题中信息补全条形统计图.
(2)学校现有800名学生,请根据图中信息,估算全校学生希望参加活动A有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=3,AC=4,BC=5,P 为边 BC 上一动点,PE⊥AB 于 E,PF⊥AC于 F,M 为 EF 中点,则 AM 的最小值为( )

A.1B.1.3C.1.2D.1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求解下列各题:
(1)先化简,再求值:5(a2b + 2ab2)- 2(3a2b + 4ab2-1),其中|a-2|+(b+ 3)2= 0:
(2)解方程:![]() =1-
=1-![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.观察下面的点阵图和相应的等式,探究其中的规律:
(1)下图反映了任何一个三角形数是如何得到的,认真观察,并在④后面的横线上写出相应的等式;
![]()

(2)通过猜想,写出(1)中与第八个点阵相对应的等式 ;
(3)从下图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.结合(1)观察下列点阵图,并在⑤看面的横线上写出相应的等式.


(4)通过猜想,写出(3)中与第n个点阵相对应的等式 ;
(5)判断256是不是正方形数,如果不是,说明理由;如果是,256可以看作哪两个相邻的“三角形数”之和?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB交x轴于点A(a,0),交![]() 轴于点
轴于点![]() ,且
,且![]() ,
,![]() 满足
满足![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .
.
(1)![]() ________;
________;![]() ________;并求直线
________;并求直线![]() 的解析式;
的解析式;
(2)过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com