【题目】钓鱼岛是我国渤海海峡上的一颗明珠，渔产丰富．一天某渔船离开港口前往该海域捕鱼．捕捞一段时间后，发现一外国舰艇进入我国水域向钓鱼岛驶来，渔船向渔政部门报告，并立即返航．渔政船接到报告后，立即从该港口出发赶往钓鱼岛．下图是渔船及渔政船与港口的距离s和渔船离开港口的时间t之间的函数图象．（假设渔船与渔政船沿同一航线航行）

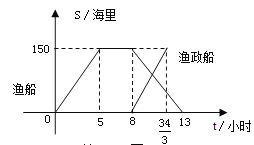
（1）直接写出渔船离港口的距离s和它离开港口的时间t的函数关系式．

（2）求渔船和渔政船相遇时，两船与钓鱼岛的距离．

（3）在渔政船驶往钓鱼岛的过程中，求渔船从港口出发经过多长时间与渔政船相距30海里？

参考答案：

【答案】（1）当0≤t≤5时，s=30 ；当5＜t≤8时，s=150；当8＜t≤13时，s=－30t+390；（2）60；（3）9．6

小时或10．4小时

【解析】

试题分析：（1）分三种情况写出函数解析式，（2）首先利用待定系数法求出渔政船离港口的距离与渔船离开港口的时间的函数关系式，然后进行计算；（3）分相遇前和相遇之后两种情况分别求出t的值．

试题解析：（1）当0≤t≤5时，s=30；当5＜t≤8时，s=150；当8＜t≤13时，s=－30t+390；

（2）渔政船离港口的距离与渔船离开港口的时间的函数关系式设为s=kt+b

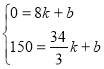解得： k=45 b=－360 ∴s=45t－360

解得 t=10 s=90

渔船离钓鱼岛距离为 150－90=60 （海里）

（3） S渔=－30t+390 S渔政=45t－360

分两种情况：

遇之前,S渔－S渔政=30

－30t+390－（45t－360）=30

解得t=（或9．6）

相遇之后,S渔政－S渔=30

45t－360－（－30t+390）=30

解得 t=（或10．4）

∴当渔船离开港口9．6小时或10．4小时时，两船相距30海里．

关闭