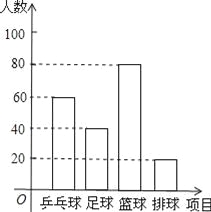
【题目】某中学综合实践活动组为了解学生最喜欢的球类运动，对足球、乒乓球、篮球、排球四个项目进行了调查，并将调查的结果绘制成如下的两幅统计图（说明：每位同学只选一种自己最喜欢的球类），请你根据图中提供的信息解答下列问题：

（1）求这次接受调查的学生人数，并补全条形统计图；

（2）求扇形统计图中喜欢排球的圆心角度数；

（3）若调查到爱好“乒乓球”的5名学生中有3名男生，2名女生，现从这5名学生中任意抽取2名学生，请用列表法或画树状图的方法，求出刚好抽到一男一女的概率．

参考答案：

【答案】

【1】200人

【2】36°

【3】

【解析】试题分析：（1）读图可知喜欢足球的有40人，占20%，所以一共调查了40÷20%=200人，

（2）先求出喜欢乒乓球的人数所占的百分比，即可求出喜欢排球的百分比，进而求出其所占圆心角的度数；

（3）用列表法或画树状图的求出总的事件所发生的数目，根据概率公式即可求出刚好抽到一男一女的概率．

试题解析：（1）∵喜欢足球的有40人，占20%，

∴一共调查了：40÷20%=200（人），

∵喜欢乒乓球人数为60（人），

∴所占百分比为：×%=30%，

∴喜欢排球的人数为：200×（1﹣20%﹣30%﹣40%）=20（人），

由以上信息补全条形统计图得：

（2）由（1）可知喜欢排球所占的百分比为：×100%=10%，

∴占的圆心角为：10%×360°=36°；

（3）画图得：

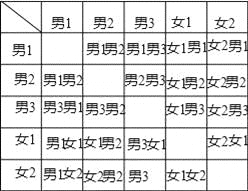
由图可知总有20种等可能性结果，其中抽到一男一女的情况有12种，所以抽到一男一女的概率为

P（一男一女）==．

关闭