练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，一个二次函数的图象经过点A、C、B三点，点A的坐标为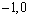（），点B的坐标为（3,0），点C在y轴的正半轴上，且AB=OC．

    （1）求点C的坐标；

    （2）求这个二次函数的解析式，并求出该函数的最大值．


    解：（1）∵  A(1，0)、B(3，0)，

    ∴ AO=1， OB=3，即AB= AO+OB=1+3=4.

    ∴ OC＝4，即点C的坐标为（0，4）.

    （2）解：设图象经过A、C、B三点的二次函数的解析式为，把A、C、B三点的坐标分别代入上式，得    解得

    ∴ 所求的二次函数解析式为．

    ∵ 点A、B的坐标分别为点A、B，

    ∴ 线段AB的中点坐标为，即抛物线的对称轴为直线．

    ∵  ，∴  当时，y有最大值.

    （本题也可设抛物线的顶点式或交点式来解答）


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    方程的根为 （    ）

       A.x=       B.x=0       C.x1=2，     D.x=或x=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知xy>0，且x2－2xy－3y2＝0，则＝        ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知反比例函数y＝的图象如左图所示，则二次函数y＝的图象大致为：

     


               A             B               C                D

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知点A（-3，y1），B（-2，y2），C（3，y3）都在反比例函数y=的图象上，则y1，y2，y3的大小关系是                       .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


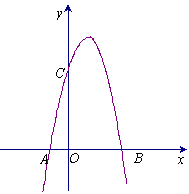
    如图，小李在一次高尔夫球选拔赛中，从山坡下O点打出一球向球洞A点飞去，球的飞行路线为抛物线，如果不考虑空气阻力，当球达到最大水平高度12米时，球移动的水平距离为9米．已知山坡OA与水平方向OC的夹角为30o，O、A两点相距8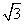米．

    （1）求直线OA的解析式；

    （2）求出球的飞行路线所在抛物线的解析式；

    （3）判断小李这一杆能否把高尔夫球从O点直接打入球洞A点.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    化简：的结果是（　　）

    　 A． 2﹣a B． ﹣2﹣a C．  D．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


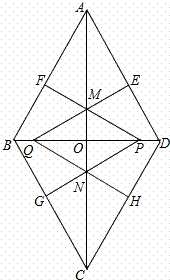
    菱形ABCD的对角线AC，BD相交于点O，AC=4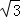，BD=4，动点P在线段BD上从点B向点D运动，PF⊥AB于点F，四边形PFBG关于BD对称，四边形QEDH与四边形PFBG关于AC对称．设菱形ABCD被这两个四边形盖住部分的面积为S1，未被盖住部分的面积为S2，BP=x．

    （1）用含x的代数式分别表示S1，S2；

    （2）若S1=S2，求x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    （﹣+1﹣）×（﹣24）

    查看答案和解析>>

    同步练习册答案