
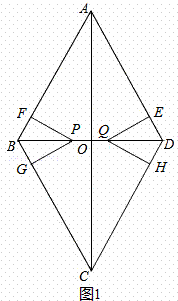
菱形ABCD的对角线AC,BD相交于点O,AC=4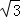 ,BD=4,动点P在线段BD上从点B向点D运动,PF⊥AB于点F,四边形PFBG关于BD对称,四边形QEDH与四边形PFBG关于AC对称.设菱形ABCD被这两个四边形盖住部分的面积为S1,未被盖住部分的面积为S2,BP=x.
,BD=4,动点P在线段BD上从点B向点D运动,PF⊥AB于点F,四边形PFBG关于BD对称,四边形QEDH与四边形PFBG关于AC对称.设菱形ABCD被这两个四边形盖住部分的面积为S1,未被盖住部分的面积为S2,BP=x.
(1)用含x的代数式分别表示S1,S2;
(2)若S1=S2,求x的值.
解:(1)①当点P在BO上,0<x≤2时,如图1所示.
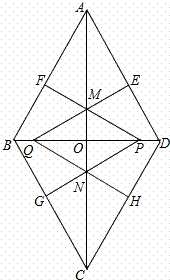
∵四边形ABCD是菱形,AC=4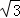 ,BD=4,
,BD=4,
∴AC⊥BD,BO=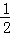 BD=2,AO=
BD=2,AO=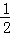 AC=2
AC=2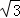 ,
,
且S菱形ABCD=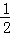 BD•AC=8
BD•AC=8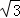 .
.
∴tan∠ABO=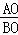 =
= .
.
∴∠ABO=60°.
在Rt△BFP中,
∵∠BFP=90°,∠FBP=60°,BP=x,
∴sin∠FBP=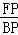 =
=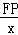 =sin60°=
=sin60°=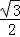 .
.
∴FP=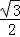 x.
x.
∴BF=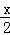 .
.
∵四边形PFBG关于BD对称,
四边形QEDH与四边形PEBG关于AC对称,
∴S△BFP=S△BGP=S△DEQ=S△DHQ.
∴S1=4S△BFP
=4×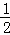 ×
×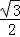 x•
x•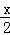
=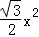 .
.
∴S2=8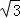 ﹣
﹣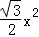 .
.
②当点P在OD上,2<x≤4时,如图2所示.
∵AB=4,BF=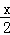 ,
,
∴AF=AB﹣BF=4﹣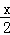 .
.
在Rt△AFM中,
∵∠AFM=90°,∠FAM=30°,AF=4﹣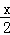 .
.
∴tan∠FAM=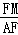 =tan30°=
=tan30°= .
.
∴FM=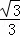 (4﹣
(4﹣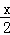 ).
).
∴S△AFM=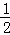 AF•FM
AF•FM
=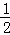 (4﹣
(4﹣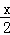 )•
)•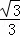 (4﹣
(4﹣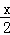 )
)
=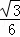 (4﹣
(4﹣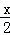 )2.
)2.
∵四边形PFBG关于BD对称,
四边形QEDH与四边形FPBG关于AC对称,
∴S△AFM=S△AEM=S△CHN=S△CGN.
∴S2=4S△AFM
=4×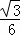 (4﹣
(4﹣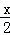 )2
)2
=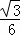 (x﹣8)2.
(x﹣8)2.
∴S1=8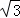 ﹣S2=8
﹣S2=8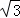 ﹣
﹣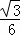 (x﹣8)2.
(x﹣8)2.
综上所述:
当0<x≤2时,S1= ,S2=8
,S2=8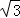 ﹣
﹣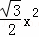 ;
;
当2<x≤4时,S1=8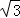 ﹣
﹣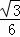 (x﹣8)2,S2=
(x﹣8)2,S2=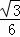 (x﹣8)2.
(x﹣8)2.
(2)①当点P在BO上时,0<x≤2.
∵S1=S2,S1+S2=8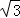 ,
,
∴S1=4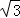 .
.
∴S1=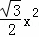 =4
=4 .
.
解得:x1=2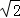 ,x2=﹣2
,x2=﹣2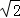 .
.
∵2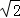 >2,﹣2
>2,﹣2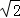 <0,
<0,
∴当点P在BO上时,S1=S2的情况不存在.
②当点P在OD上时,2<x≤4.
∵S1=S2,S1+S2=8 ,
,
∴S2=4 .
.
∴S2=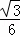 (x﹣8)2=4
(x﹣8)2=4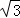 .
.
解得:x1=8+2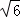 ,x2=8﹣2
,x2=8﹣2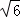 .
.
∵8+2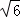 >4,2<8﹣2
>4,2<8﹣2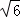 <4,
<4,
∴x=8﹣2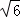 .
.
综上所述:若S1=S2,则x的值为8﹣2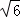 .
.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
如图所示,在数轴上点A所表示的数x的范围是( )
A. sin30°<x<sin60°;B.cos30°<x<
sin30°<x<sin60°;B.cos30°<x<  cos45°;
cos45°;
C. tan30°<x<tan45°;D.3cos60°<x<
tan30°<x<tan45°;D.3cos60°<x<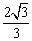 tan60°。
tan60°。
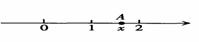
查看答案和解析>>
科目:初中数学 来源: 题型:
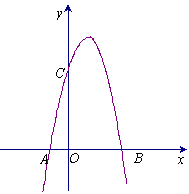
如图,一个二次函数的图象经过点A、C、B三点,点A的坐标为(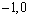 ),点B的坐标为(3,0),点C在y轴的正半轴上,且AB=OC.
),点B的坐标为(3,0),点C在y轴的正半轴上,且AB=OC.
(1)求点C的坐标;
(2)求这个二次函数的解析式,并求出该函数的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
若点P1(﹣1,y1),P2(﹣2,y2),P3(1,y3),都在函数y=x2﹣2x+3的图象上,则( )

A.y2<y1<y3 B.y1<y2<y3 C.y2>y1>y3 D.y1>y2>y3
查看答案和解析>>
科目:初中数学 来源: 题型:
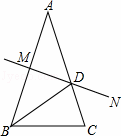
如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,有下面3个结论:①BD是∠ABC的角平分线;②△BCD是等腰三角形;③△AMD≌△BCD.
其中正确的结论有__________(只需填写正确结论的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com