
����Ŀ��ij�������м���ԭ��360ǧ�ˣ�����ԭ��290ǧ�ˣ��ƻ�����������ԭ������A��B���ֲ�Ʒ50��������һ��A��Ʒ��Ҫ����ԭ��9ǧ�ˣ�����ԭ��3ǧ�ˣ��ɻ�����700Ԫ������һ��B��Ʒ����Ҫ����ԭ��4ǧ�ˣ�����ԭ��10ǧ�ˣ��ɻ�����1200Ԫ��
��1��������x��A�ֲ�Ʒ��д��������xӦ����IJ���ʽ�飻
��2�����������ļ��ְ�Ҫ����A��B���ֲ�Ʒ��������������������������������Ƴ�����
���𰸡���1��![]() ����2����3����������������1��A��Ʒ30����B��Ʒ20��������2��A��Ʒ31����B��Ʒ19��������3��A��Ʒ32����B��Ʒ18����
����2����3����������������1��A��Ʒ30����B��Ʒ20��������2��A��Ʒ31����B��Ʒ19��������3��A��Ʒ32����B��Ʒ18����
����������������1��������x��A�ֲ�Ʒ��������B��Ʒ��50��x����������Ҫ����ԭ��[9x+4��50��x��]ǧ��������ԭ��[3x+10��50��x��]ǧ������������Ϳ��Խ�������ʽ����
��2�������1���IJ���ʽ��Ľ⼯���Ϳ���ȷ��x��ֵ���Ӷ��������������
�������1��������x��A�ֲ�Ʒ��������B��Ʒ��50��x����������Ҫ����ԭ��[9x+4��50��x��]ǧ��������ԭ��[3x+10��50��x��]ǧ�������������
![]() ��
��
��2����![]() �������30��x��32����x��������x=30��31��32������3������������
�������30��x��32����x��������x=30��31��32������3������������
����1��A��Ʒ30����B��Ʒ20����
����2��A��Ʒ31����B��Ʒ19����
����3��A��Ʒ32����B��Ʒ18����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����������y= ![]() ��x��0����ͼ����һ�κ� ��y=��x+b��ͼ��ֱ���A��1��3����B���㣮
��x��0����ͼ����һ�κ� ��y=��x+b��ͼ��ֱ���A��1��3����B���㣮
��1����m��b��ֵ��
��2������M�Ƿ���������ͼ���ϵ�һ���㣬ֱ��MC��x����C����ֱ��AB�ڵ�N��MD��y����D��NE��y����E�����ı���MDOC��NEOC������ֱ�ΪS1��S2 �� S=S2��S1 �� ��S�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ADƽ�֡�BAC��BC�ڵ�D����F��BA���ӳ����ϣ���E���߶�CD�ϣ�EF��AC�ཻ�ڵ�G����BDA+��CEG=180�㣮
��1��AD��EFƽ������˵�����ɣ�
��2������H��FE���ӳ����ϣ��ҡ�EDH=��C�����F���H�������˵�����ɣ�
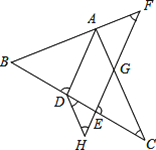
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC��BDƽ����ABC��AC�ڵ�D��AE��BD��CB���ӳ����ڵ�E������E=35��������BAC�Ķ���Ϊ��������

A. 40�� B. 45�� C. 60�� D. 70��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ṩ��˼·�㲦������գ�Ȼ����ɽ���ȫ����.
��ͼ����֪AB��AD����BAD��60������BCD��120�����ӳ�BC��ʹCE��CD������DE����֤��BC+DC��AC.
˼·�㲦����1������֪����AB��AD����BAD��60������֪��ABD�ǣ�������.ͬ������֪������BCD��120���õ���DCE���ߣ���CE��CD����֪�ߣ�
��2��Ҫ֤BC+DC��AC���ɽ�����ת��Ϊ֤�����߶���ȣ����ߣ��ߣ�
��3��Ҫ֤��2��������д�������߶���ȣ�������֤����.��д��������֤������.
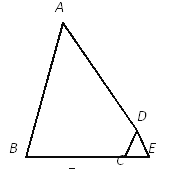
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��У����5���������2��С�������������ԣ�ͬʱ����1���������2��С�������ɹ�1680��ѧ���Ͳͣ�ͬʱ����2���������1��С�������ɹ�2280��ѧ���Ͳ͡�
��1��1���������1��С�����ֱ�ɹ�������ѧ���Ͳͣ�
��2����7������ͬʱ���ţ��ܷ�ȫУ��5300��ѧ���Ͳͣ���˵������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ίԱͳ����ȫ��ͬѧ60�������Ĵ��������г��������������ֲ������ش��������⣺
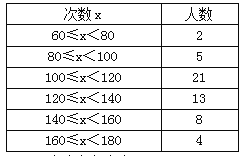
��1��ȫ���ж����ˣ�
��2����ࡢ�����Ƕ��٣�
��3������������100��x��140��Χ��ͬѧ�ж����ˣ�ռȫ��İٷ�֮������ȷ��0.01%����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ�У�������A1B1C1O1��A2B2C2C1������AnBnCnCn��1����ͼ��ʾ�ķ�ʽ���ã����е�A1��A2��A3������An����һ�κ���y=kx+b��ͼ���ϣ���C1��C2��C3������Cn����x���ϣ�����B1������Ϊ��1��1������B2������Ϊ��3��2�������An������Ϊ �� 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com