
 的一边在BC上,其余两个顶点E、F分别在AB、AC上.
的一边在BC上,其余两个顶点E、F分别在AB、AC上.| EH |
| AD |
| BE |
| AB |
| EF |
| BC |
| AE |
| AB |
| EF |
| BC |
| AK |
| AD |
| EH |
| AD |
| BE |
| AB |
| EF |
| BC |
| AE |
| AB |
| x |
| 24 |
| BE |
| AB |
| x |
| 16 |
| AE |
| AB |
| x |
| 24 |
| x |
| 16 |
| BE |
| AB |
| AE |
| AB |
| 48 |
| 5 |
| 72 |
| 5 |
| 72 |
| 5 |
| EF |
| BC |
| AK |
| AD |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |


科目:初中数学 来源: 题型:
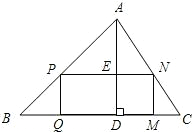 下再拼成(不计接缝用料及损耗)与长方形PQMN大小一样的长方形?若能,试给出一种拼法;若不能,试说明理由.
下再拼成(不计接缝用料及损耗)与长方形PQMN大小一样的长方形?若能,试给出一种拼法;若不能,试说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
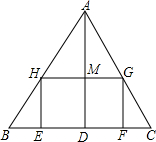 一个长HG是宽HE的2倍的矩形EFGH.使它的一边EF在BC上,顶点G,H分别在AC,AB上.AD与HG的交点为M.
一个长HG是宽HE的2倍的矩形EFGH.使它的一边EF在BC上,顶点G,H分别在AC,AB上.AD与HG的交点为M.| AM |
| AD |
| HG |
| BC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
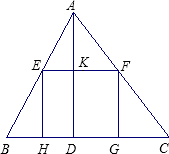 的一边在BC上,其余两个顶点E、F分别在AB、AC上.
的一边在BC上,其余两个顶点E、F分别在AB、AC上.查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(45):2.4 二次函数的应用(解析版) 题型:解答题
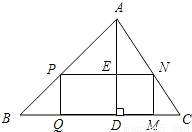
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com