
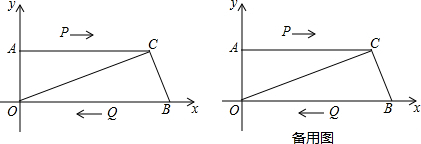
���� ��1��������y=ax��x-40����Ȼ���ɵ�C��36��12����������y=ax��x-40���ϣ������ô���ϵ�����Ϳ�������κ����Ľ���ʽ��
��2����PQ=BC�ɷ��ı���PCBQ��ƽ���ı��κ͵���������������������ۣ��Ϳ��Խ�����⣮
��3���ֱ���PQΪƽ���ı��εıߺͶԽ��߽������ۣ��Ϳɽ�����⣮
���  �⣺��1����ͼ1���������y=ax��x-40����
�⣺��1����ͼ1���������y=ax��x-40����
�ߵ�C��36��12����������y=ax��x-40���ϣ�
��a��36����36-40��=12��
��ã�a=-$\frac{1}{12}$��
��y=-$\frac{1}{12}$x��x-40��=-$\frac{1}{12}$x2+$\frac{10}{3}$x��
���O��C��B����������ߵĽ���ʽΪy=-$\frac{1}{12}$x2+$\frac{10}{3}$x�� ��2�������ı���PCBQ��ƽ���ı��Σ���ͼ2��
��2�������ı���PCBQ��ƽ���ı��Σ���ͼ2��
����PC=BQ��
��AP=t��BQ=2t��AC=36��OB=40��
��36-t=2t��
��ã�t=12��
�����ı���PCBQ�ǵ������Σ�
����P��PG��OB������ΪG����ͼ3��
���ı���PCBQ�ǵ������Σ�
��PQ=CB����PQG=��CBH��
��Rt��PGQ��Rt��CHB��
$\left\{\begin{array}{l}{��PQG=��CBH}\\{��PGQ=��CHB}\\{PQ=CB}\end{array}\right.$��
��Rt��PGQ��Rt��CHB��AAS����
��GQ=BH��PG=CH��
�ߡ�PGH=��CHB=90�㣮
��PG��CH��
���ı���PCHG��ƽ���ı��Σ�
��PC=GH��
��36-t=2t-2��4��
��ã�t=$\frac{44}{3}$��
������������tΪ12���$\frac{44}{3}$��ʱ��PQ=BC�� ��3����PQΪƽ���ı��ε�һ���ߣ�
��3����PQΪƽ���ı��ε�һ���ߣ�
�����ı���OPQM��ƽ���ı��Σ���ͼ4�٣�
����P��PR��OB������ΪR������M��MS��OB������ΪS��
���ı���OPQM��ƽ���ı��Σ�
��PQ��OM��PQ=OM��
���MOQ=��PQO��
���SOM=��RQP��
�ڡ�OSM�͡�QRP�У�
$\left\{\begin{array}{l}{��SOM=��RQP}\\{��OSM=��QRP}\\{OM=PQ}\end{array}\right.$��
���OSM�ա�QRP��AAS����
��SM=RP��OS=QR��
��RP=12��
��SM=12��
��yM=-12��
��-$\frac{1}{12}$x2+$\frac{10}{3}$x=-12��
��ã�x1=20+4$\sqrt{34}$����ȥ����x2=20-4$\sqrt{34}$��
��ʱ��M������Ϊ��20-4$\sqrt{34}$��-12����
QR=OS=4$\sqrt{34}$-20��
OQ=OR-QR=AP-QR=t-��4$\sqrt{34}$-20��=40-2t��
��ã�t=$\frac{20+4\sqrt{34}}{3}$��
�����ı���OQPM��ƽ���ı��Σ���ͼ4�ڣ�
����PM=OQ��
��y=12ʱ��-$\frac{1}{12}$x2+$\frac{10}{3}$x=12��
��ã�x1=4��x2=36����ȥ����
��ʱ��M������Ϊ��4��12����
PM=t-4��OQ=40-2t��
����t-4=40-2t��
��ã�t=$\frac{44}{3}$�� ��PQΪƽ���ı��ε�һ���Խ��ߣ���ͼ5��
��PQΪƽ���ı��ε�һ���Խ��ߣ���ͼ5��
���ı���OPMQ��ƽ���ı��Σ�
��PM��OQ��PM=OQ��
�ߵ�M����PC�ϣ������������ϣ�
���M���C�غϣ�����M������Ϊ��36��12����
��PM=OQ��36-t=40-2t��
��ã�t=4��
������������t=$\frac{20+4\sqrt{34}}{3}$ʱ��M��20-4$\sqrt{34}$��-12������t=$\frac{44}{3}$ʱ��M��4��12������t=4ʱ��M��36��12����
���� ���⿼�����ô���ϵ��������κ����Ľ���ʽ��ƽ���ı��ε����ʡ��������ε����ʡ�ȫ�������ε��ж������ʡ����ɶ��������涨����֪ʶ��ע���������������Ӧ��ͼ���ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
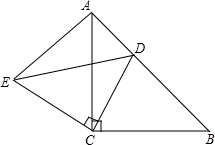 ��֪����ͼ����ABC�͡�ECD���ǵ���ֱ�������Σ���ACD=��DCE=90�㣬DΪ�߶�AB��һ���㣮
��֪����ͼ����ABC�͡�ECD���ǵ���ֱ�������Σ���ACD=��DCE=90�㣬DΪ�߶�AB��һ���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
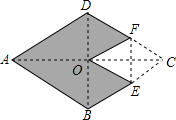 ��ͼ������ABCD�У�AC��BD�ཻ�ڵ�O����������EF�۵���ʹ��C���O�غϣ���AC=8��BD=6����ͼ����Ӱ���ֵ����Ϊ18��
��ͼ������ABCD�У�AC��BD�ཻ�ڵ�O����������EF�۵���ʹ��C���O�غϣ���AC=8��BD=6����ͼ����Ӱ���ֵ����Ϊ18���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
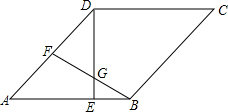 ��ͼ��������ABCD�У���A=60�㣬E��F�ֱ���AB��AD���е㣬DE��BF�ཻ�ڵ�G������CG��
��ͼ��������ABCD�У���A=60�㣬E��F�ֱ���AB��AD���е㣬DE��BF�ཻ�ڵ�G������CG���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ������ABCD�У�AE��BC�ڵ�E��AF��CD�ڵ�F����E��F�ֱ�ΪBC��CD���е㣬���EAF���ڣ�������
������ABCD�У�AE��BC�ڵ�E��AF��CD�ڵ�F����E��F�ֱ�ΪBC��CD���е㣬���EAF���ڣ�������| A�� | 60�� | B�� | 55�� | C�� | 45�� | D�� | 30�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com