
 如图,点P是直线l:y=-2x-2上的点,过点P的另一条直线m交抛物线y=x2于A、B两点,试证明:对于直线l上任意给定的一点P,在抛物线上都能找到点A,使得PA=AB成立.
如图,点P是直线l:y=-2x-2上的点,过点P的另一条直线m交抛物线y=x2于A、B两点,试证明:对于直线l上任意给定的一点P,在抛物线上都能找到点A,使得PA=AB成立. 分析 首先设P(a,-2a-2),A(m,m2),再表示出B点坐标,进而利用根的判别式求出,无论a为何值时,关于m的方程总有两个不相等的实数根,进而得出答案.
解答 证明:设P(a,-2a-2),A(m,m2).
如图所示,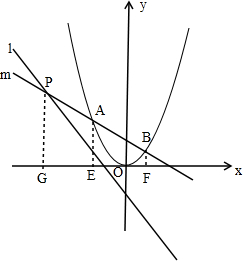
分别过点P、A、B作x轴的垂线,垂足分别为点G、E、F.
∵PA=AB,∴AE是梯形PGFB的中位线,
∴GE=EF,AE=$\frac{1}{2}$(PG+BF).
∵OF=|EF-OE|,GE=EF,
∴OF=|GE-EO|
∵GE=GO-EO=m-a,EO=-m,
∴OF=|m-a-(-m)|=|2m-a|,
∴OF=2m-a,
∵AE=$\frac{1}{2}$(PG+BF),
∴BF=2AE-PG=2m2+2a+2,
可得:B(2m-a,2m2+2a+2).
∵点B在抛物线y=x2上,
∴2m2+2a+2=(2m-a)2
整理得:2m2-4am+a2-2a-2=0.
△=8(a+1)2+8>0,
∴无论a为何值时,关于m的方程总有两个不相等的实数根.
即对于任意给定的点P,抛物线上总能找到满足条件的点A,使得PA=AB成立.
点评 本题考查二次函数与一次函数的图象与性质、梯形及梯形中位线、一元二次方程等知识点,掌握二次函数、一次函数点的坐标特征,正确表示出B点坐标是解题关键.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:解答题
 如图,螺旋形是由一系列直角三角形组成的,其中OA=OA1=A1A2=…=An-1An=1.AAn表示直角三角形的斜边,Sn表示第n个三角形的面积.则:
如图,螺旋形是由一系列直角三角形组成的,其中OA=OA1=A1A2=…=An-1An=1.AAn表示直角三角形的斜边,Sn表示第n个三角形的面积.则:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=$\frac{1}{2}$x2+bx+c与直线l:y=kx+m交于A(4,2)、B(0,-1)两点.
如图,抛物线y=$\frac{1}{2}$x2+bx+c与直线l:y=kx+m交于A(4,2)、B(0,-1)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
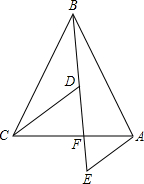 如图,在△ABC中,BC=BA,点F是AC上一点.点D是BF上一点,且∠CDF=∠CBA,AE∥CD交BF延长线于E.探究线段BD与EA的数量关系.
如图,在△ABC中,BC=BA,点F是AC上一点.点D是BF上一点,且∠CDF=∠CBA,AE∥CD交BF延长线于E.探究线段BD与EA的数量关系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com