
分析 (1)根据1×2+2×3+3×4=$\frac{1}{3}$×3×4×5=20可以得出,连续两个自然数的乘积的和等于后面一个算式的两个数字再与最后一个数字加1相乘积的$\frac{1}{3}$,据此可计算1×2+2×3+…+100×101;
(2)由此得出一般性规律1×2+2×3+…+n(n+1)=$\frac{1}{3}$n(n+1)(n+2)即可解决问题.
解答 解:(1)∵1×2+2×3+3×4=$\frac{1}{3}$×3×4×5=$\frac{1}{3}$×4×5=20,
∴1×2+2×3+…+100×101=$\frac{1}{3}$×100×101×102=343400;
(2)1×2+2×3+3×4+…+n×(n+1)=$\frac{1}{3}$n(n+1)( n+2).
故答案为:(1)343400;(2)$\frac{1}{3}$n(n+1)(n+2).
点评 此题主要考查了数字的规律性问题,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,很容易发现各部分的变化规律,但是如何用一个统一的式子表示出变化规律是难点中的难点.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
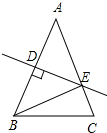 在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,若∠EBC=30°,则∠A的度数为( )
在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,若∠EBC=30°,则∠A的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
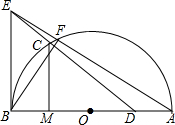 如图,在半径为2的⊙O中,AB是直径,C是弧AB的三等分点(∠BOC为锐角),D是OA的中点,BE是⊙O的切线,B为切点,DC的延长线交BE于点E,连接AE,交⊙O于点F.
如图,在半径为2的⊙O中,AB是直径,C是弧AB的三等分点(∠BOC为锐角),D是OA的中点,BE是⊙O的切线,B为切点,DC的延长线交BE于点E,连接AE,交⊙O于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com