
| FM |
| EM |
| FM |
| EM |
| 3 |
| FM |
| EM |
| FM |
| EM |
3
| ||
| 2 |
3
| ||
| 2 |
| 3 |
| FM |
| EM |
| ||
| 2 |
| ||
| 2 |
| FM |
| EM |
| AO |
| BO |
| ||
| 3 |
| DO |
| CO |
| ||
| 3 |
| AO |
| BO |
| DO |
| CO |
| ||
| 3 |
| AD |
| BC |
| ||
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| EF |
| FM |
| ||
| 3 |
| EF |
| FM |
| ||
| 3 |
| FM |
| EM |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
3
| ||
| 2 |
3
| ||
| 2 |
3
| ||
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
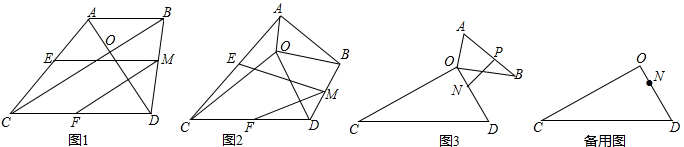
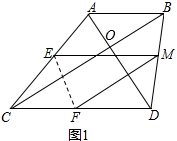
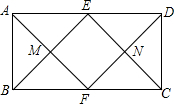 如图,在矩形ABCD中,E,F分别是AD,BC中点,连接AF,BE,CE,DF分别交于点M,N,四边形EMFN是( )
如图,在矩形ABCD中,E,F分别是AD,BC中点,连接AF,BE,CE,DF分别交于点M,N,四边形EMFN是( )| A、正方形 | B、菱形 |
| C、矩形 | D、无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
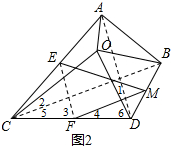
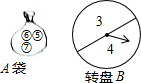 学习概率知识以后,小庆和小丽设计了一个游戏.在一个不透明的布袋A里面装有三个分别标有数字5,6,7的小球(小球除数字不同外,其余都相同);同时制作了一个可以自由转动的转盘B,转盘B被平均分成2部分,在每一部分内分别标上数字3,4.现在其中一人从布袋A中随机摸取一个小球,记下数字为x;另一人转动转盘B,转盘停止后,指针指向的数字记为y(若指针指在边界线上时视为无效,重新转动),从而确定点P的坐标为P(x,y).
学习概率知识以后,小庆和小丽设计了一个游戏.在一个不透明的布袋A里面装有三个分别标有数字5,6,7的小球(小球除数字不同外,其余都相同);同时制作了一个可以自由转动的转盘B,转盘B被平均分成2部分,在每一部分内分别标上数字3,4.现在其中一人从布袋A中随机摸取一个小球,记下数字为x;另一人转动转盘B,转盘停止后,指针指向的数字记为y(若指针指在边界线上时视为无效,重新转动),从而确定点P的坐标为P(x,y).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com