练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如下图，在锐角△ABC中，CD，BE分别是AB，AC边上的高，且CD，BE相交于一点P，若∠A=50 °，则∠BPC=
    [     ]
    A．150°
    B．130 °
    C．120 °
    D．100 °
    B
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    26、探究题
    如下图所示，已知平面内A、B、C、D、E五个点．
    （1）按要求画出图形：
    ①画直线AC；
    ②画射线EA、EC；
    ③连接AB、BC、CD、DA．
    （2）在（1）所画的图形中，任意找出一个锐角和一个钝角，并将它们分别表示出来：
    锐角：
    ∠EAC

    钝角：
    ∠AEC

    （3）①用量角器量出四边形AECD的四个内角的度数，即∠DAE、∠AEC、∠ECD、∠CDA的度数分别为
    50°，150°，60°，90°
    ，这四个内角的度数和为
    360°
    ；
    ②用量角器量出四边形ABCD的四个内角的度数，即∠DAB、∠ABC、∠BCD、∠CDA的度数分别为
    90°，70°，110°，90°
    ，这四个内角的度数和为
    360°
    ．从以上的操作中，你有什么发现？（只需写出结论）

    查看答案和解析>>

    科目：初中数学 来源：2011年甘肃兰州市初中毕业生学业考试数学试卷 题型：044

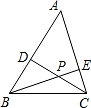
    通过学习三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做顶角正对(sad)，如下图，在△ABC中，AB＝AC，顶角A的正对记作sadA，这时sadA＝底边/腰＝．容易知道一个角的大小与这个角的正对值也是相互唯一确定的．根据上述角的正对定义，解下列问题：

    (1)sad60°＝________．

    (2)对于0°＜A＜180°，∠A的正对值sadA的取值范围是________．

    (3)如下图，已知sinA＝，其中∠A为锐角，试求sadA的值．

    查看答案和解析>>

    科目：初中数学 来源：2009年黑龙江省哈尔滨市中考数学试题 题型：044

    如下图，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点A的坐标为(－3，4)，点C在x轴的正半轴上，直线AC交y轴于点M，AB边交y轴于点H．

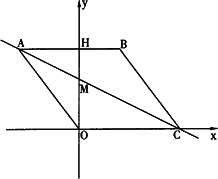
    (1)求直线AC的解析式；

    (2)连接BM，如下图，动点P从点A出发，沿折线ABC方向以2个单位／秒的速度向终点C匀速运动，设△PMB的面积为S(S≠0)，点P的运动时间为t秒，求S与t之间的函数关系式(要求写出自变量t的取值范围)；

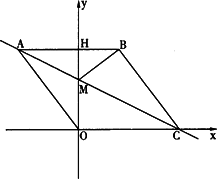
    (3)在(2)的条件下，当t为何值时，∠MPB与∠BCO互为余角，并求此时直线OP与直线AC所夹锐角的正切值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如下图，矩形ABCD中，AB = 8，BC = 10，点P在矩形的边DC上由D向C运动．沿直线AP翻折△ADP，形成如下四种情形．设DP = x，△ADP和矩形重叠部分（阴影）的面积为y．

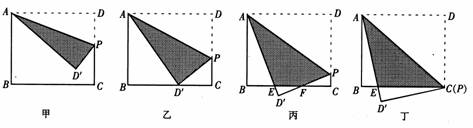
    （1）如图丁，当点P运动到与C重合时，求重叠部分的面积y；

    （2）如图乙，当点P运动到何处时，翻折△ADP后，点D恰好落在BC边上？这时重叠部分的面积y等于多少？

    （3）阅读材料：

    已知锐角a≠45°，tan2a 是角2a 的正切值，它可以用角a 的正切值tana 来表示，即

              （a≠45°）．

    根据上述阅读材料，求出用x表示y的解析式，并指出x的取值范围．（提示：在图丙中可设∠DAP = a ）

    查看答案和解析>>

    同步练习册答案