
如图,在直角坐标系xoy中,O是坐标原点,点A在x正半轴上,OA= cm,点B在y轴的正半轴上,OB=12cm,动点P从点O开始沿OA以
cm,点B在y轴的正半轴上,OB=12cm,动点P从点O开始沿OA以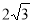 cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s.
cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s.
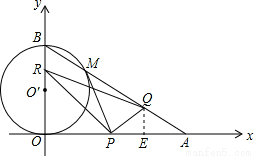
(1)求∠OAB的度数.
(2)以OB为直径的⊙O‘与AB交于点M,当t为何值时,PM与⊙O‘相切?
(3)求出△PQR的面积S随动点移动时间t的函数关系式,并求s的最小值及相应的t值.
(1)30°;(2)3;(3)3.
【解析】
试题分析:(1)在Rt△OAB中,已知了OA、OB的长,即可求出∠OAB的正切值,由此可得到∠OAB的度数;
(2)连接O′M,当PM与⊙O′相切时,PM、PO同为⊙O′的切线,易证得△OO′P≌△MO′P,则∠OO′P=∠MO′P;在(1)中易得∠OBA=60°,即△O′BM是等边三角形,由此可得到∠BO′M=∠PO′M=∠PO′O=60°;在Rt△OPO′中,根据∠PO′O的度数及OO′的长即可求得OP的长,已知了P点的运动速度,即可根据时间=路程÷速度求得t的值;
(3)过Q作QE⊥x轴于E,在Rt△AQE中,可用t表示出AQ的长,进而根据∠OAB的度数表示出QE、AE的长,由S△PQR=S△OAB-S△OPR-S△APQ-S△BRQ即可求得S、t的函数关系式;根据所得函数的性质及自变量的取值范围即可求出S的最小值及对应的t的值.
试题解析:(1)在Rt△AOB中:
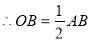
∴∠OAB=30°
(2)如图,连接O‘P,O‘M.当PM与⊙O‘相切时,
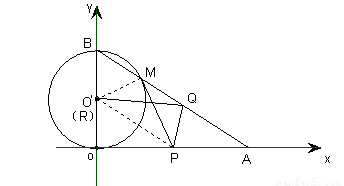
有∠PM O‘=∠PO O‘=90°,
△PMO‘≌△POO‘由(1)知∠OBA=60°
∵O‘M= O‘B ∴△O‘BM是等边三角形
∴∠B O‘M=60°
可得∠O O‘P=∠M O‘P=60°
∴
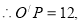
 OP=
OP=
又∵OP=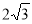 t
t
∴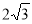 t=
t=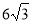 ,t=3
,t=3
即:t=3时,PM与⊙O‘相切
(3)如图,过点Q作QE⊥x于点E

∵∠BAO=30°,AQ=4t
∴QE= AQ=2t AE=
AQ=2t AE=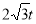
∴OE=OA-AE= -
-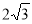 t
t
∴Q点的坐标为( -
-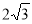 t,2t)
t,2t)
S=S△PQR= S△OAB -S△OPR -S△APQ -S△BRQ
=
= (
( )
)
∵S= =
= (
( )
)
双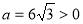 ,抛物线开口向上
,抛物线开口向上
∴当t=3时,S最小值=
考点:圆的综合题.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源:2013-2014学年黑龙江省绥棱县九年级(五四制)上学期期末考试数学试卷(解析版) 题型:选择题
原价为 元的某商品经过两次降价后,现售价
元的某商品经过两次降价后,现售价 元,如果每次降价的百分比都为
元,如果每次降价的百分比都为 ,则下列各式正确的是( )
,则下列各式正确的是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年辽宁省大石桥市中考模拟考试数学试卷(解析版) 题型:选择题
如图是由七个相 同的小正方体摆成的几何体,则这个几何体的俯视图是( )


A. B. C. D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年福建省南平市中考模拟数学试卷(解析版) 题型:填空题
一个圆形转盘被平均分成红、黄、蓝3个扇形区域,向其投掷一枚飞镖,飞镖落在红色区域的概率是 。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年福建省南平市中考模拟数学试卷(解析版) 题型:选择题
已知点P(1,﹣3)在反比例函数 (k≠0)的图象上,则k的值是( )
(k≠0)的图象上,则k的值是( )
A.3 B.﹣3 C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖南省长沙市九年级下学期期中考试数学试卷(解析版) 题型:解答题
我市实施新课程改革后,学生的自主学习、合作交流能力有很大提高,张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
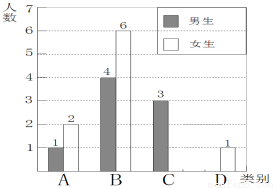
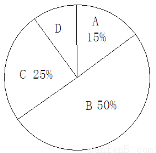
(1)本次调查中,张老师一共调查了 名同学,并将上面的条形统计图补充完整。
(2)为了共同进步,张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖南省长沙市九年级下学期期中考试数学试卷(解析版) 题型:填空题
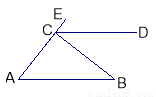
如图,BC⊥AE,垂足为C,过C作CD∥AB.若∠ECD=48°,则∠B=__________.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省宁波市九年级上学期第一次月考数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系中,反比例函数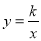 (x>0)的图象和矩形ABCD的第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).
(x>0)的图象和矩形ABCD的第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).
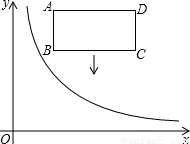
(1)直接写出B、C、D三点的坐标;
(2)若将矩形向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求矩形的平移距离和反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省宁波市九年级上学期期中考试数学试卷(解析版) 题型:选择题
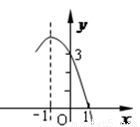
如图, 抛物线 的部分图象如图所示,若
的部分图象如图所示,若 ,则
,则 的取值范围是( )
的取值范围是( )
A.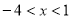 B.
B. C.
C. 或
或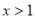 D.
D. 或
或
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com