分析:由于△OP
1A
1是等腰直角三角形,过点P
1作P
1M⊥x轴,则P
1M=OM=MA
1,所以可设P
1的坐标是(a,a),把(a,a)代入解析式得到a=3,从而求出A
1的坐标是(6,0),再根据△P
2A
1A
2是等腰直角三角形,设P
2的纵坐标是b,则P
2的横坐标是6+b,把(6+b,b)代入函数解析式得到b=
,解得b=3
-3,则A
2的横坐标是6
,同理可以得到A
3的横坐标是6
,A
n的横坐标是6
,根据等腰三角形的性质得到y
1+y
2+…y
n等于An点横坐标的一半,因而值是3
.
解答:
解:如图,过点P
1作P
1M⊥x轴,
∵△OP
1A
1是等腰直角三角形,
∴P
1M=OM=MA
1,
设P
1的坐标是(a,a),
把(a,a)代入解析式y=
(x>0)中,得a=3,
∴A
1的坐标是(6,0),
又∵△P
2A
1A
2是等腰直角三角形,
设P
2的纵坐标是b,则P
2的横坐标是6+b,
把(6+b,b)代入函数解析式得b=
,
解得b=3
-3,
∴A
2的横坐标是6+2b=6+6
-6=6
,
同理可以得到A
3的横坐标是6
,
A
n的横坐标是6
,
根据等腰三角形的性质得到y
1+y
2+…y
n等于A
n点横坐标的一半,
∴y
1+y
2+…y
n=
3.
故答案为:
3.
点评:本题是等腰直角三角形与反比例函数相结合的题目,关键是要分析出其图象特点,再结合反比例函数性质作答.

 如图所示,P1(x1,y1)、P2(x2,y2),…Pn(xn,yn)在函数y=
如图所示,P1(x1,y1)、P2(x2,y2),…Pn(xn,yn)在函数y= 解:如图,过点P1作P1M⊥x轴,
解:如图,过点P1作P1M⊥x轴,

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案 如图所示,P1(x1,y1)、P2(x2,y2),…Pn(xn,yn)在函数y=
如图所示,P1(x1,y1)、P2(x2,y2),…Pn(xn,yn)在函数y= 如图所示,P1(x1,y1)、P2(x2,y2),…P10(x10,y10)在函数y=
如图所示,P1(x1,y1)、P2(x2,y2),…P10(x10,y10)在函数y= 的图象上,△OP1A1,△P2A1A2,△P3A2A3……△PnAn-1An……都是等腰直角三角形,斜边OA1,A1A2……An-1An,都在x轴上, 则y1+y2+…yn= 。
的图象上,△OP1A1,△P2A1A2,△P3A2A3……△PnAn-1An……都是等腰直角三角形,斜边OA1,A1A2……An-1An,都在x轴上, 则y1+y2+…yn= 。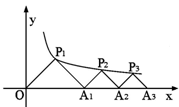
 (x>0)的图象上,△OP1A1,△P2A1A2,△P3A2A3…△PnAn-1An…都是等腰直角三角形,斜边OA1,
(x>0)的图象上,△OP1A1,△P2A1A2,△P3A2A3…△PnAn-1An…都是等腰直角三角形,斜边OA1,