
分析 (1)前面1到9,都是一位数,故有9位,后面接下来从10到98每个数都是两位,总共有(98-9)×2=89×2=178位数,所以1到98总共要178+9=187位数;
(2)前面1到9位数,是1到9的和,后面接下来是10个1的和,再接下来是0到9的和,再接下来是10个2的和,再接下来是0到9的和,…,最后是10个9的和以及0到9的和,所以各个位上的数字之间和为10(1+2+3+4+5+6+7+8+9)×2-9×2=882;
(3)根据两个数的和和两个数的差的奇偶性是相同的,所以若干次后剩余数的差和98个数的和的奇偶性相同,根据1、2、3、…98的和是(1+98)×98÷2=4851是奇数,2016不是奇数,所以没有这种可能性.
解答 解:(1)9+(98-9)×2
=9+178
=187,
所以,这个新数是一个187位数;
(2)10(1+2+3+4+5+6+7+8+9)×2-9×2
=10×45×2-18
=900-18
=882;
(3)由于两个数的和和两个数的差的奇偶性是相同的,
所以若干次后剩余数的差和98个数的和的奇偶性相同,
因为1+2+3+…+98=(1+98)×98÷2=4851是奇数,
2016不是奇数,所以没有这种可能性.
点评 本题考查了学生对数的构成、对大数的认识以及分析能力;两个数的和和两个数的差的奇偶性是相同的是解(3)的关键.


科目:初中数学 来源: 题型:解答题
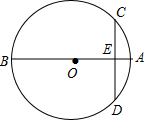 ⊙O的两条弦AB,CD相交于点E.
⊙O的两条弦AB,CD相交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
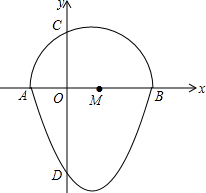 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象的开口向下 | B. | 图象的对称轴为直线x=$\frac{3}{2}$ | ||
| C. | 函数的最大值为1 | D. | 当x>2时,y随x的增大而增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 第一年 | 第二年 | 第三年 | … | |
| 应还款(万元) | 3 | 0.5+9×0.4% | 0.5+8.5×0.4% | … |
| 剩余房款(万元) | 9 | 8.5 | 8 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com