
【题目】如图,A,O,B三点在同一直线上,∠BOD与∠BOC互补.

(1)试判断∠AOC与∠BOD之间有怎样的数量关系,写出你的结论,并加以证明;
(2)OM平分∠AOC,ON平分∠AOD,①依题意,将备用图补全;
② 若∠MON=40°,求∠BOD的度数.
【答案】(1)∠AOC =∠BOD ;(2)①答案见解析;②∠BOD =50°.
【解析】试题分析:(1)根据同角的补角相等即可得出结论;
(2)①根据题意画出图形;
②由角平分线的定义和平角的定义解答即可.
试题解析:解:(1)∠AOC =∠BOD .理由如下:
∵ 点A,O,B三点在同一直线上, ∴ ∠AOC +∠BOC = 180°.
∵∠BOD与∠BOC互补,∴ ∠BOD +∠BOC = 180°,∴ ∠AOC =∠BOD.
(2)①补全图形,如图所示.
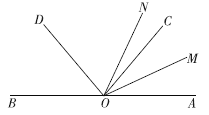
②设∠AOM =α.
∵ OM平分∠AOC,∴ ∠AOC =2∠AOM =2α.
∵ ∠MON=40°,∴ ∠AON =∠MON +∠AOM =40°+ α.
∵ ON平分∠AOD,∴ ∠AOD =2∠AON =80° +2α.
由(1)可得 ∠BOD=∠AOC=2α,∵∠BOD +∠AOD =180°,∴ 2α+ 80 +2α=180°,∴ 2α=50°,∴ ∠BOD =50°.


科目:初中数学 来源: 题型:
【题目】如图,直线L: ![]() 与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.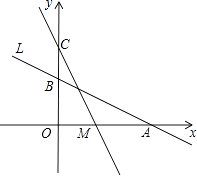
(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,并求此时M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
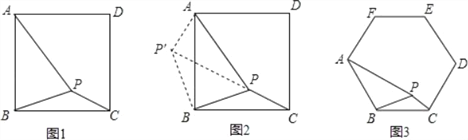
【题目】如图1,在正方形ABCD内有一点P,PA=3,PB=2,PC=1,求∠BPC的度数.
分析:根据已知条件比较分散的特点,我们可以通过旋转变换将分散的已知条件集中在一起,于是将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图2),然后连结PP′,这时再分别求出∠BP′P和∠AP′P的度数.
解答:(1)请你根据以上分析再通过计算求出图2中∠BPC的度数;
(2)如图3,若在正六边形ABCDEF内有一点P,且PA=2![]() ,PB=4,PC=2,求∠BPC的度数.
,PB=4,PC=2,求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AOB是一条直线,OC是∠AOD的平分线,OE 是∠BOD的平分线.
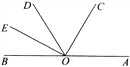
(1)若∠AOE=140°,求∠AOC的度数;
(2)若∠EOD :∠COD=2 : 3,求∠COD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为8的等边![]() 和等边
和等边![]() 互相重合,现将
互相重合,现将![]() 沿直线
沿直线![]() 向左平移
向左平移![]() 个单位,将
个单位,将![]() 沿直线
沿直线![]() 向右平移
向右平移![]() 个单位.
个单位.
(1)若![]() =2,则BE= ;
=2,则BE= ;
(2)当![]() 、
、![]() 是线段
是线段![]() 的三等分点时,则
的三等分点时,则![]() 的值为多少.
的值为多少.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com