
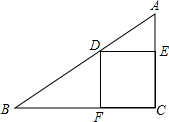
 在Rt△ABC中,四边形DECF为正方形,若AD=5,DB=6,则△ADE与△BDF的面积之和为________.
在Rt△ABC中,四边形DECF为正方形,若AD=5,DB=6,则△ADE与△BDF的面积之和为________. x,BF=
x,BF= x,
x, •AE•DE+
•AE•DE+ •BF•DF=
•BF•DF= x2,
x2, x)2=52,
x)2=52,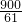 ,
, ×
×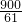 =15,
=15,

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
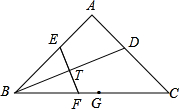 如图,在Rt△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别与AB,BC交于点E,F,在线段BC上取一点G,使CG=CD.
如图,在Rt△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别与AB,BC交于点E,F,在线段BC上取一点G,使CG=CD.查看答案和解析>>
科目:初中数学 来源: 题型:
 我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法.请你用等面积法来探究下列两个问题:
我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法.请你用等面积法来探究下列两个问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com