Question

问题情境：
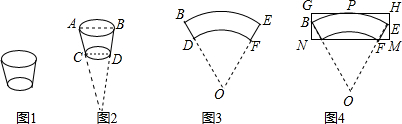
小明和小颖在吃冰淇淋时，对其所用的一次性纸杯（如图1）产生了兴趣，决定对制做这种纸杯的相关问题进行研究，他们发现纸杯是圆台形状（即一个大圆锥截去一个小圆锥后余一的部分，如图2），并测得杯口直径AB=8cm，杯底直径CD=6cm，杯壁母线长AC=BD=6cm，说明：整个探究过程中均忽略纸杯的接接部分和纸杯的厚度．

数学理解：
（1）为进一步探究问题的本质，小颖画出纸杯的侧面展开的大致图形，如图3，得到的图形是圆环的一部分，那么，图3中

BE

的长为

 

cm，

DF

的长为

 

cm．
（2）小明认为，要想准确画出纸杯的侧面展开图，需要确定图3中

BE

和

DF

所在圆的半径OE，OF的长以及圆心角∠BOE的度数，小颖根据弧长的计算公式猜想得到

BE 的长

DF 的长

=

OE

OF

，请你证明这个结论，并根据这个结论，求

DF

所在圆的半径OF及它所对的圆心角∠BOE的度数．
问题解决：
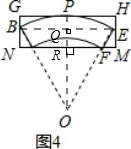
（3）明确了纸杯侧面展开图的有关数据和图形的性质后，他们继续探究将原材料截前成纸杯侧面的方案，并给出了方案，将原材料剪成矩形纸片，再按如图4所示的方式剪出这个纸杯的侧面，其中，扇形OBE的

BE

与矩形GHMN的边GH相切于点P，点P是

BE

的中点，点B，E，F，D均在矩形的边上，请直接写出矩形纸片的长和宽．

Answer 1

考点：圆的综合题

专题：

分析：（1）立体平面图形转化中，可见

BE

的长即为杯口圆的周长，而

DF

的长即为杯底圆的周长．由已知杯口直径AB=8cm，杯底直径CD=6cm，结论易得．
（2）求证

BE 的长

DF 的长

=

OE

OF

，一般我们都考虑分别用OE，OF表示出

BE

的长和

DF

的长，然后相除后再找其与

OE

OF

的关系．
    求OF，题中已提示利用上述公式．因为（1）我们已知等式的左边，右边OE可否用OF表示呢？观察图已知，OE=OF+杯壁母线长，又杯壁母线长AC=BD=6cm，所以结果易得．
（3）求矩形纸片的长与宽，直接考虑都在扇形外，所以可以考虑转化到扇形中，由P为圆的切点，一般连接圆心与切点，如是连接OP，连接BE，记两线交于Q，记OP与MN交于点R．此时BE即为矩形的长，PR即为矩形的宽，其中又由圆心角为60°，易得△OBE为等边三角形，则BE可求．同时△ROF为含30°角的直角三角形，边长易得，进而PR易得．

解答：解：
（1）8π，6π．

（2）证明：设

BE

与

DF

所对的圆心角为n°．
∴

BE

的长=

n

360

•2π•OE=

nπ

180

•OE，

DF

的长=

n

360

•2π•OF=

nπ

180

•OF，
∴

BE 的长

DF 的长

=

nπ 180

nπ 180

•

OE

OF

=

OE

OF

．
∵OE=OF+6，

BE

的长=8π，

DF

的长=6π，
∴

8π

6π

=

OF+6

OF

，
解得，OF=18，
∴OE=OF+6=18+6=24．
∵

DF

的长=

nπ

180

•OF=6π，OF=18，
∴n=60．
所以，所在圆的半径OF等于18cm，它所对的圆心角的度数为60°．

（3）
答：矩形纸片的长GH=24cm，宽GN=(24-9

3

)cm．
分析如下：

在图4中，连接OP，连接BE，两线交于Q，OP与MN交于点R．此时由图形对称可知，PO⊥BE，PO⊥NM，
∵OB=OE，∠BOE=60°，
∴△BOE为等边三角形，则BE=OE=24，
∴矩形纸片的长GH=24cm．
∵∠BOE=60°，
∴∠FOR=30°，
在Rt△FOR中，
∵OF=18，
∴RF=9，
∴OR=9

3

，
∴PR=OP-OR=24-9

3

，
∴矩形纸片的宽GN=(24-9

3

)cm．

点评：本题首先考查了学生的空间思维能力，能否清晰的找准空间图形与平面图形之间的对应关系．另外主要考查了弧长、圆心角、半径之间的关系及利用特殊直角三角形求边长等内容．本题虽然长，内容多，图多，但是考查知识点都比较基础，能够有效的锻炼学生的读题理解能力，总体来说是到不错的题目．