
 如图在△ABC中,AB=5,AC=3,BC=4,P从A点出发,沿射线AC运动,速度为每秒2个单位长度,Q点从C点出发,沿射线CB运动,速度为每秒1个单位长度,若点P,Q同时出发,经过时间t后,△PQC与△ABC相似,求运动时间.
如图在△ABC中,AB=5,AC=3,BC=4,P从A点出发,沿射线AC运动,速度为每秒2个单位长度,Q点从C点出发,沿射线CB运动,速度为每秒1个单位长度,若点P,Q同时出发,经过时间t后,△PQC与△ABC相似,求运动时间.| CP |
| AC |
| CQ |
| CB |
| 3-2t |
| 3 |
| t |
| 4 |
| 12 |
| 11 |
| CP |
| CB |
| CQ |
| CA |
| 3-2t |
| 4 |
| t |
| 3 |
| 9 |
| 10 |
| 12 |
| 11 |
| 9 |
| 10 |


科目:初中数学 来源: 题型:
 在我校举行九年的级季篮球赛上,九年级(1)班的啦啦队队员,为了在明天的比赛中给本班同学加油助威,提前每人制作了一面同一规格的直角三角形彩旗.队员小明放学回家后,发现自己的彩旗破损了一角,他想重新制作一面彩旗.请你帮助小明,用直尺与圆规在作出一个与破损前完全一样的三角形(保留作图痕迹,不写作法).
在我校举行九年的级季篮球赛上,九年级(1)班的啦啦队队员,为了在明天的比赛中给本班同学加油助威,提前每人制作了一面同一规格的直角三角形彩旗.队员小明放学回家后,发现自己的彩旗破损了一角,他想重新制作一面彩旗.请你帮助小明,用直尺与圆规在作出一个与破损前完全一样的三角形(保留作图痕迹,不写作法).查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,以格点为端点的线段叫格点线段,点A、B均在边长为1的网格的格点上,将格点线段AB先水平向左平移1个单位,再向上平移2个单位.
如图,以格点为端点的线段叫格点线段,点A、B均在边长为1的网格的格点上,将格点线段AB先水平向左平移1个单位,再向上平移2个单位.查看答案和解析>>
科目:初中数学 来源: 题型:
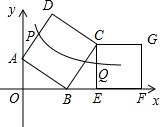 如图,正方形ABCD和正方形CEFG各有两个顶点在坐标轴上,其中A(0,1),B(2,0),E、F两点同在x轴上,双曲线y=
如图,正方形ABCD和正方形CEFG各有两个顶点在坐标轴上,其中A(0,1),B(2,0),E、F两点同在x轴上,双曲线y=| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
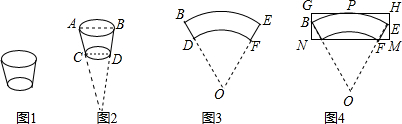
 |
| BE |
 |
| DF |
 |
| BE |
 |
| DF |
| ||
|
| OE |
| OF |
 |
| DF |
 |
| BE |
 |
| BE |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com