
| A. | 2x3+5x-1和-9x3-3x-3 | B. | 5x3+x+8和-12x3+x-12 | ||
| C. | -3x3+x+5和-4x3+x-1 | D. | -7x3+3x-2和-x-2 |
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
 甲驾车从A地去往B地,到达后停留3个小时,然后返回,往返车速都为120千米/时,乙驾车从B地去往A地,到达后停留1.5小时,因事提前返回,乙往返的车速不变,如图是两车距A地的路程s(千米0与行驶时间t(小时)之间的函数图象,请结合图象回答下列问题:
甲驾车从A地去往B地,到达后停留3个小时,然后返回,往返车速都为120千米/时,乙驾车从B地去往A地,到达后停留1.5小时,因事提前返回,乙往返的车速不变,如图是两车距A地的路程s(千米0与行驶时间t(小时)之间的函数图象,请结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知两条直线l1、l2分别经过点A(-1,0)、点B(3,0)并且当两条直线同时相交于y轴的负半轴上的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l1交于点K,与直线l2交于点E,在x轴交于点F,D是抛物线的顶点,如图所示.
已知两条直线l1、l2分别经过点A(-1,0)、点B(3,0)并且当两条直线同时相交于y轴的负半轴上的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l1交于点K,与直线l2交于点E,在x轴交于点F,D是抛物线的顶点,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,下列条件中,不能证明△ABC≌△DCB的是( )
如图,下列条件中,不能证明△ABC≌△DCB的是( )| A. | AB=CD,AC=BD | B. | AB=CD,∠ABC=∠BCD | C. | ∠ABC=∠DCB,∠A=∠D | D. | AB=CD,∠A=∠D |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
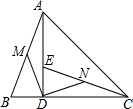 如图,在△ABC中,AD⊥BC,垂足为D,AD=CD,点E在AD上,DE=BD,M、N分别是AB、CE的中点.
如图,在△ABC中,AD⊥BC,垂足为D,AD=CD,点E在AD上,DE=BD,M、N分别是AB、CE的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com