我市某学习机营销商经营某品牌A、B两种型号的学习机.用10000元可进货A型号的学习机5个,B型号的学习机10个;用11000元可进货A型号的学习机10个,B型号的学习机5个.
(1)求A、B两种型号的学习机每个分别为多少元?
(2)若该学习机营销商销售1个A型号的学习机可获利120元,销售1个B型号的学习机可获利90元,该学习机营销商准备用不超过30000元购进A、B两种型号的学习机共40个,且这两种型号的学习机全部售出后总获利不低于4440元,问有几种进货方案?这几种进货方案中,该学习机营销商将这些型号的学习机全部售出后,获利最大的是哪种方案?最大利润是多少?
解:(1)设A、B两种型号的学习机每个分别为x元、y元,由题意,得
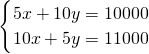
,
解得:

.
答:A、B两种型号的学习机每个分别为800元、600元;
(2)设购A型号的学习机a个,则购进B型号的学习机(40-a)个,由题意,得
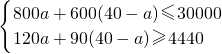
,
解得:28≤a≤30,
∵a为整数,
∴a=28,29,30.
∴共有3种购买方案:
方案1:A型号学习机28个,B型号学习机12;
方案2:A型号学习机29个,B型号学习机11;
方案3:A型号学习机30个,B型号学习机10;
设总利润为W元,由题意,得
W=120a+90(40-a)=30a+3600.
∴k=30>0,
∴W随a的增大而增大,
∴a=30时,W
最大=4500元.
分析:(1)设A、B两种型号的学习机每个分别为x元、y元,根据A型学习机的价格+B型学习机的价格=总价建立方程组求出其解即可;
(2)设购A型号的学习机a个,则购进B型号的学习机(40-a)个,根据购买的费用建立不等式为:800a+600(40-a)≤30000,根据利润的数量关系建立不等式为120a+90(40-a)≥4440,从而建立不等式组求出其解就可以得出进货方案,设总利润为W元,由两种型号的学习机的总利润=W建立关系,由一次函数的性质求出其解即可.
点评:本题考查了列二元一次方程组解实际问题的运用,一元一次不等式组解实际问题的运用,一次函数的性质的运用,设计方案的运用,解答时建立方程组和不等式组是解答的关键.

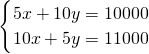 ,
, .
.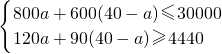 ,
,

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案