
 x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
 x2 + bx-2上,∴
x2 + bx-2上,∴ × (-1 )2 + b× (-1)–2 = 0,解得b =
× (-1 )2 + b× (-1)–2 = 0,解得b =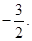
 x2-
x2-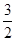 x-2. y=
x-2. y= x2-
x2-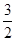 x-2 =
x-2 = ( x2 -3x- 4 ) =
( x2 -3x- 4 ) = (x-
(x-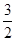 )2-
)2-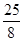 ,
,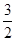 , -
, -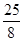 ).
).  x2-
x2-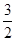 x-2 = 0, ∴x1 =" -1," x2 = 4, ∴B (4,0)
x-2 = 0, ∴x1 =" -1," x2 = 4, ∴B (4,0)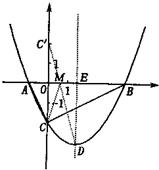
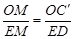
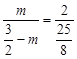 ,∴m =
,∴m =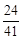 .
.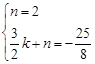 ,解得n =" 2,"
,解得n =" 2,"  .
.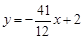 .
.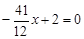 ,
,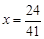 . ∴
. ∴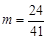 .
.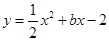 过A(-1,0)点,直接求出b的值,再根据配方法求出二次函数顶点坐标即可;
过A(-1,0)点,直接求出b的值,再根据配方法求出二次函数顶点坐标即可;

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源:不详 题型:解答题
 时,
时, 有最大值为5,且它的图象经过点(2,3),求:
有最大值为5,且它的图象经过点(2,3),求: 不小于3时,请直接写出对应的自变量
不小于3时,请直接写出对应的自变量 的取值范围.
的取值范围.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
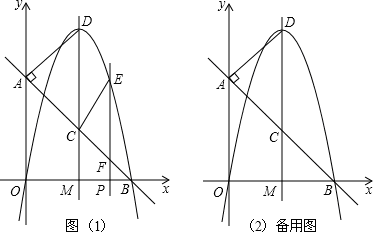
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 (a≠0)于x轴有一个交点的横坐标x的范围是( )
(a≠0)于x轴有一个交点的横坐标x的范围是( ) | x | 3.23 | 3.24 | 3.25 | 3.26 |
| y | ﹣0.06 | ﹣0.02 | 0.03 | 0.09 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com