
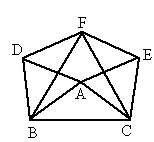
如图所示,△EFC是△ABC绕点C顺时针旋转,60°得到的图形,△DBF是△ABC绕点B逆时针旋转60°得到的图形.
(1)请说明四边形AEFD是平行四边形;
(2)想一想,当△ABC满足什么条件时,以点A、E、F、D为顶点的四边形不存在?
|
解: (1)由于△EFC和△DBF都是由△ABC旋转得到的,根据旋转的特征,有AB=EF=DB.又由于∠ ABD=60°,所以△ABD为等边三角形.所以 AB=DB=AD,于是EF=AD.同理可得,△ ACE为等边三角形,AE=DF.由两组对边分别相等的四边形是平行四边形, 所以四边形 AEFD为平行四边形.(2) 当∠BAC=60°时,∠ DAE=360°-∠DAB-∠EAC-∠BAC=360 °-60°-60°-60°=180 °.此时点 D、A、E在同一条直线上,故以A、E、F、D为顶点的四边形不存在. |
|
本题既考查了图形旋转变换的特征,又考查了特殊平行四边形的判定方法,由一般到特殊,层层设问,实在是一道好题.当然本题应从图形的旋转变换入手,根据旋转的特征,得到△ ABC与△EFC、△DBF之间的边与边的相等关系,从而达到说明四边形AEFD是平行四边形.然后由“有一个角是直角的平行四边形是矩形”来探索△ABC应具有的特征,由“有一组邻边相等的平行四边形是菱形”来探索△ABC应满足的条件.根据上面两问的讨论不难发现,当∠ABC=60°时,D、A、E三点在同一直线上,即以A、E、F、D为顶点的四边形不存在. |


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:044
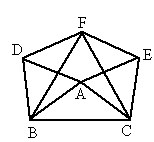
如图所示,△EFC是△ABC绕点C顺时针旋转60°得到的图形,△DBF是△ABC绕点B逆时针旋转60°得到的图形.
(1)请说明四边形AEFD是平行四边形;
(2)想一想,当△ABC满足什么条件时,以点A、E、F、D为顶点的四边形不存在?
查看答案和解析>>
科目:初中数学 来源: 题型:
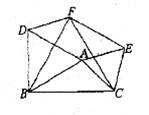
如图所示,△EFC是△ABC绕点C顺时针旋转60°得到的图形,△DBF是△ABC绕点B逆时针旋转60°得到的图形。
(1)请你说明四边形AEFD是平行四边形。
(2)想一想,当△ABC满足什么条件时,四边形AEFD是菱形?矩形?
(3)探索一下,当△ABC满足什么条件时,以A、E、F、D为顶点的四边形不存在?为什么?
查看答案和解析>>
科目:初中数学 来源:湖北省期中题 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com