
【题目】分解因式:
(1)a2b-abc; (2)3a(x-y)+9(y-x);
(3)(2a-b)2+8ab; (4)(m2-m)2+![]() (m2-m)+
(m2-m)+![]() .
.
【答案】(1)ab(a-c);(2)3(x-y)(a-3);(3)(2a+b)2;(4)(m-![]() )4.
)4.
【解析】
(1)提取公因式ab,即可解答;
(2)先把原式变形为3a(x-y)-9(x-y),再提取公因式3(x-y),即可解答;
(3)根据整式的乘法、合并同类项,可得完全平方公式,根据完全平方公式,可得答案;
(4)把(m2-m)看作一个整体,然后利用完全平方公式分解因式即可.
(1)原式=ab(a-c);
(2)原式=(x-y)(3a-9)=3(x-y)(a-3);
(3)原式=4a2-4ab+b2+8ab=4a2+4ab+b2=(2a+b)2;
(4)原式=(m2-m)2+2·(m2-m)·![]() +
+![]() 2=(m2-m+
2=(m2-m+![]() )2=[(m-
)2=[(m-![]() )2]2=(m-
)2]2=(m-![]() )4.
)4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
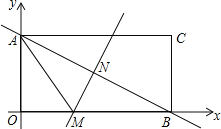
【题目】如图,长方形AOBC在直角坐标系中,点A在y轴上,点B在x轴上,已知点C的坐标是(8,4).
(1)对角线AB的垂直平分线MN交x轴于点M,连接AM,求线段AM的长;
(2)在x轴上是否存在一个点P,使△PAM为等腰三角形?如果有请直接写出符合题意的所有点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
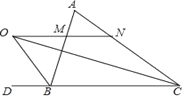
【题目】如图,已知在△ABC中,△ABC的外角∠ABD的平分线与∠ACB的平分线交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N.
求证:(1)MO=MB;(2)MN=CN﹣BM.
查看答案和解析>>
科目:初中数学 来源: 题型:
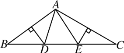
【题目】如图,在△ABC中,AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,连接AD,AE.
(1)若∠BAC=110°,求∠DAE的度数;
(2)若∠BAC=θ(0°<θ<180°),求∠DAE的度数.(用含θ的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
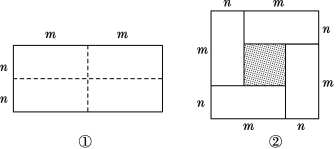
【题目】图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀把它均分成四个小长方形,然后按图②的形状拼成一个正方形.
(1)你认为图②中的阴影部分的正方形的边长等于多少?
(2)请用两种不同的方法求图②中阴影部分的面积.
(3)观察图②你能写出下列三个代数式之间的等量关系吗?
代数式:(m+n)2,(m-n)2,mn.
(4)根据(3)题中的等量关系,解决如下问题:
已知a+b=7,ab=5,求(a-b)2的值.(写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
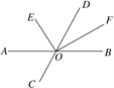
【题目】如图,直线AB、CD交于点O,OE平分∠AOD,OF平分∠BOD.
(1)∠AOC=50°,求∠DOF与∠DOE的度数,并计算∠EOF的度数;
(2)当∠AOC的度数变化时,∠EOF的度数是否变化?若不变,求其值;若变化,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com