
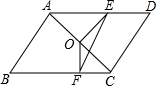
 如图,?ABCD中,O为对角线AC的中点,AC⊥AB,点E为AD中点,并且OF⊥BC,∠D=53°,则∠FOE的度数是( )
如图,?ABCD中,O为对角线AC的中点,AC⊥AB,点E为AD中点,并且OF⊥BC,∠D=53°,则∠FOE的度数是( )| A. | 37° | B. | 53° | C. | 127° | D. | 143° |
分析 首先根据平行四边形的性质得到:∠BAC=∠DCA=90°,然后根据点O为AC的中点,点E为AD的中点利用中位线定理得到OE∥CD,从而得到∠AOE=∠ACD=90°,然后根据OF⊥BC得到∠FOC=∠B=53°,从而得到∠EOF=∠EOC+∠FOC=90°+53°=143°.
解答 解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∵AC⊥AB,
∴∠BAC=∠DCA=90°,
∵点O为AC的中点,点E为AD的中点,
∴OE∥CD,
∴∠COE+∠ACD=180°,
∴∠COE=90°
∵∠D=∠B=53°,OF⊥BC,
∴∠FOC=∠B=53°,
∴∠EOF=∠EOC+∠FOC=90°+53°=143°,
故选D.
点评 本题考查了平行四边形的性质,解题的关键是能够根据题意并利用中位线定理确定答案.


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:选择题
| A. | (x-y)(x+y)=x2-y2 | B. | a2-4a+4=a(a-4)+4 | ||
| C. | m2n-8n=n(m+4)(m-4) | D. | 3(a-b)+a(b-a)=(a-b)(3-a) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,某同学探究n边形的内角和公式,首先将以顶点A1为端点的对角线A1A3、A1A4、A1A5、A1A6、…、A1An-1连接,将此n边形分割成(n-2)个三角形,然后由每个三角形的内角和为180°,可得n边形的内角和为(n-2)-180°.该同学的上述探究方法所体现的数学思想是( )
如图,某同学探究n边形的内角和公式,首先将以顶点A1为端点的对角线A1A3、A1A4、A1A5、A1A6、…、A1An-1连接,将此n边形分割成(n-2)个三角形,然后由每个三角形的内角和为180°,可得n边形的内角和为(n-2)-180°.该同学的上述探究方法所体现的数学思想是( )| A. | 分类讨论 | B. | 公理化 | C. | 类比 | D. | 转化 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将抛物线y=x2向右平移a个单位长度,顶点为A,与y轴交于点B,且△AOB为等腰直角三角形.
如图,将抛物线y=x2向右平移a个单位长度,顶点为A,与y轴交于点B,且△AOB为等腰直角三角形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②④ | B. | ①③④ | C. | ①②③ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | B. | $\sqrt{-3}$×$\sqrt{-2}$=$\sqrt{6}$ | C. | $\sqrt{12}$-$\sqrt{3}$=$\sqrt{3}$ | D. | $\sqrt{8}$÷$\sqrt{2}$=4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com