
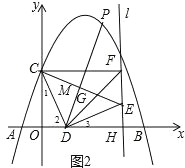
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=ax2+bx+3НЛxжсгкAЃЈЉ1ЃЌ0ЃЉКЭBЃЈ5ЃЌ0ЃЉЃЌНЛyжсгкЕуCЃЌЕуDЪЧЯпЖЮOBЩЯвЛЖЏЕуЃЌСЌНгCDЃЌНЋCDШЦЕуDЫГЪБеыа§зЊ90ЁуЕУЕНЯпЖЮDEЃЌЙ§ЕуEзїжБЯпlЁЭxжсЃЌДЙзуЮЊHЃЌЙ§ЕуCзїCFЁЭlгкFЃЌСЌНгDFЃЌCEНЛгкЕуGЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓЯпЖЮDFЕФГЄЃЛ
ЃЈ3ЃЉЕБDG=![]() ЪБЃЌ
ЪБЃЌ
ЂйЧѓtanЁЯCGDЕФжЕЃЛ
ЂкЪдЬНОПдкxжсЩЯЗНЕФХзЮяЯпЩЯЃЌЪЧЗёДцдкЕуPЃЌЪЙЁЯEDP=45ЁуЃПШєДцдкЃЌЧыаДГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉХзЮяЯпНтЮіЪНЮЊЃКy=Љ![]() x2+
x2+![]() x+3ЃЛЃЈ2ЃЉDF=
x+3ЃЛЃЈ2ЃЉDF=![]() =3
=3![]() ЃЛЃЈ3ЃЉЂйtanЁЯCGD=3ЃЛ
ЃЛЃЈ3ЃЉЂйtanЁЯCGD=3ЃЛ
ЂкPЕузјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉАбAЕуКЭBЕузјБъДњШыy=ax2+bx+3жаЕУЕНЙигкaЁЂbЕФЗНГЬзщЃЌШЛКѓНтЗНГЬзщЧѓГіaЁЂbМДПЩЕУЕНХзЮяЯпНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЯШЧѓГіCЕузјБъЃЌдйИљОна§зЊЕФаджЪЕУЕНCD=DEЃЌЁЯCDE=90ЁуЃЌдйжЄУїЁїOCDЁеЁїHDEЕУЕНHD=OC=3ЃЌНгзХЫЕУїЫФБпаЮOCFHЮЊОиаЮЕУЕНHF=OC=3ЃЌШЛКѓРћгУЙДЙЩЖЈРэМЦЫуDFЃЛ
ЃЈ3ЃЉЂйРћгУЁїCDEКЭЁїDFHЖМЪЧЕШбќжБНЧШ§НЧаЮЕУЕНЁЯDCE=45ЁуЃЌЁЯDFH=45ЁуЃЌгкЪЧгаЁЯDFC=45ЁуЃЌдђПЩжЄУїЁїDCGЁзЁїDFCЃЌИљОнЯрЫЦЕФаджЪЕУ![]() =
=![]() ЃЌЁЯDGC=ЁЯDCFЃЌНгзХРћгУЯрЫЦБШПЩМЦЫуГіCD=
ЃЌЁЯDGC=ЁЯDCFЃЌНгзХРћгУЯрЫЦБШПЩМЦЫуГіCD=![]() ЃЌРћгУЁЯDCF=ЁЯ2ЕУЕНЁЯCGD=ЁЯ2ЃЌШЛКѓдкRtЁїOCDжаЧѓГіЁЯ2ЕФе§ЧажЕМДПЩЕУЕНtanЁЯCGDЕФжЕЃЛ
ЃЌРћгУЁЯDCF=ЁЯ2ЕУЕНЁЯCGD=ЁЯ2ЃЌШЛКѓдкRtЁїOCDжаЧѓГіЁЯ2ЕФе§ЧажЕМДПЩЕУЕНtanЁЯCGDЕФжЕЃЛ
ЂкИљОнЁїDCGЁзЁїDFCЕУЕНHD=OC=3ЃЌEH=OD=1ЃЌдђEЃЈ4ЃЌ1ЃЉЃЌШЁCEЕФжаЕуMЃЌШчЭМ2ЃЌРћгУЯпЖЮЕФжаЕузјБъЙЋЪНЕУЕНMЃЈ2ЃЌ2ЃЉЃЌИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪХаЖЯDPОЙ§CEЕФжаЕуMЃЌНгЯТРДРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпDPЕФНтЮіЪНЮЊy=2xЉ2ЃЌШЛКѓНтЗНГЬзщ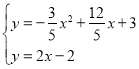 ПЩЕУPЕузјБъЃЎ
ПЩЕУPЕузјБъЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁпХзЮяЯпy=ax2+bx+3НЛxжсгкAЃЈЉ1ЃЌ0ЃЉКЭBЃЈ5ЃЌ0ЃЉЃЌ
Ёр![]() ЃЌНтЕУ
ЃЌНтЕУ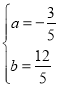 ЃЌЁрХзЮяЯпНтЮіЪНЮЊЃКy=Љ
ЃЌЁрХзЮяЯпНтЮіЪНЮЊЃКy=Љ![]() x2+
x2+![]() x+3ЃЛ
x+3ЃЛ
ЃЈ2ЃЉЕБx=0ЪБЃЌy=Љ![]() x2+
x2+![]() x+3=3ЃЌдђCЃЈ0ЃЌ3ЃЉЃЌШчЭМ1ЃЌ
x+3=3ЃЌдђCЃЈ0ЃЌ3ЃЉЃЌШчЭМ1ЃЌ
ЁпCDШЦЕуDЫГЪБеыа§зЊ90ЁуЕУЕНЯпЖЮDEЃЌ
ЁрCD=DEЃЌЁЯCDE=90ЁуЃЌ
ЁпЁЯ2+ЁЯ3=90ЁуЃЌ
ЖјЁЯ1+ЁЯ2=90ЁуЃЌ
ЁрЁЯ1=ЁЯ3ЃЌ
дкЁїOCDКЭЁїHDEжа
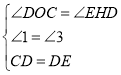 ЃЌ
ЃЌ
ЁрЁїOCDЁеЁїHDEЃЌ
ЁрHD=OC=3ЃЌ
ЁпCFЁЭBFЃЌ
ЁрЫФБпаЮOCFHЮЊОиаЮЃЌ
ЁрHF=OC=3ЃЌ
ЁрDF=![]() =3
=3![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЂйЁпЁїCDEКЭЁїDFHЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌШчЭМ1ЃЌ
ЁрЁЯDCE=45ЁуЃЌЁЯDFH=45ЁуЃЌ
ЁрЁЯDFC=45ЁуЃЌ
ЖјЁЯCDG=ЁЯFDCЃЌ
ЁрЁїDCGЁзЁїDFCЃЌ
Ёр![]() ЃЌЁЯDGC=ЁЯDCFЃЌМД
ЃЌЁЯDGC=ЁЯDCFЃЌМД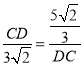 ЃЌНтЕУCD=
ЃЌНтЕУCD=![]() ЃЌ
ЃЌ
ЁпCFЁЮOHЃЌ
ЁрЁЯDCF=ЁЯ2ЃЌ
ЁрЁЯCGD=ЁЯ2ЃЌ
дкRtЁїOCDжаЃЌOD=![]() =
=![]() =1ЃЌ
=1ЃЌ
ЁрtanЁЯ2=![]() =3ЃЌ
=3ЃЌ
ЁрtanЁЯCGD=3ЃЛ
ЂкЁпOD=1ЃЌ
ЁрDЃЈ1ЃЌ0ЃЉЃЌ
ЁпЁїOCDЁеЁїHDEЃЌ
ЁрHD=OC=3ЃЌEH=OD=1ЃЌ
ЁрEЃЈ4ЃЌ1ЃЉЃЌ
ШЁCEЕФжаЕуMЃЌШчЭМ2ЃЌдђMЃЈ2ЃЌ2ЃЉЃЌ
ЁпЁїDCEЮЊЕШбќжБНЧШ§НЧаЮЃЌЁЯEDP=45ЁуЃЌ
ЁрDPОЙ§CEЕФжаЕуMЃЌ
ЩшжБЯпDPЕФНтЮіЪНЮЊy=mx+nЃЌ
АбDЃЈ1ЃЌ0ЃЉЃЌMЃЈ2ЃЌ2ЃЉДњШыЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁржБЯпDPЕФНтЮіЪНЮЊy=2xЉ2ЃЌ
НтЗНГЬзщ ЕУ
ЕУ Лђ
Лђ ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
ЁрЂкPЕузјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ



 ЪБПЬзМБИзХЪюМйзївЕдзгФмГіАцЩчЯЕСаД№АИ
ЪБПЬзМБИзХЪюМйзївЕдзгФмГіАцЩчЯЕСаД№АИ ЪюМйЯЮНгНЬВФЦкФЉЪюМйдЄЯАЮфККГіАцЩчЯЕСаД№АИ
ЪюМйЯЮНгНЬВФЦкФЉЪюМйдЄЯАЮфККГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁЯAOB=110ЁуЃЌODЦНЗжЁЯBOCЃЌOEЦНЗжЁЯAOCЃЎ 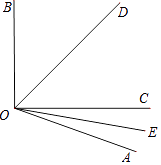
ЃЈ1ЃЉЧѓЁЯEODЕФЖШЪ§ЃЎ
ЃЈ2ЃЉШєЁЯBOC=90ЁуЃЌЧѓЁЯAOEЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКдВаФдкШ§НЧаЮЕФвЛБпЩЯЃЌгыСэвЛБпЯрЧаЃЌЧвОЙ§Ш§НЧаЮвЛИіЖЅЕуЃЈЗЧЧаЕуЃЉЕФдВЃЌГЦЮЊетИіШ§НЧаЮдВаФЫљдкБпЩЯЕФЁААщЫцдВЁБЃЎ
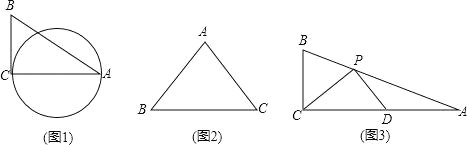
ЃЈ1ЃЉШчЭМ1ЃЌЁїABCжаЃЌЁЯC=90ЁуЃЌAB=5ЃЌBC=3ЃЌдђACБпЩЯЕФАщЫцдВЕФАыОЖЮЊ ЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌвбжЊЕШбќЁїABCЃЌAB=AC=5ЃЌBC=6ЃЌЛВнЭМВЂжБНгаДГіЫќЕФЫљгаАщЫцдВЕФАыОЖЃЎ
ЃЈ3ЃЉШчЭМ3ЃЌЁїABCжаЃЌЁЯACB=90ЁуЃЌЕуPдкБпABЩЯЃЌAP=2BPЃЌDЮЊACжаЕуЃЌЧвЁЯCPD=90ЁуЃЎ
ЂйЧѓжЄЃКЁїCPDЕФЭтНгдВЪЧЁїABCФГвЛЬѕБпЩЯЕФАщЫцдВЃЛ
ЂкЧѓcosЁЯPDCЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПРЌЛјЕФЗжРрДІРэгыЛиЪеРћгУЃЌПЩвдМѕЩйЮлШОЃЌНкЪЁзЪдДЃЎФГГЧЪаЛЗБЃВПУХЮЊСЫЬсИпаћДЋЪЕаЇЃЌГщбљЕїВщСЫВПЗжОгУёаЁЧјвЛЖЮЪБМфФкЩњЛюРЌЛјЕФЗжРрЧщПіЃЌЦфЯрЙиаХЯЂШчЭМЃК
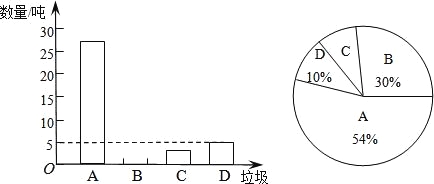
ЃЈзЂЃКAЮЊПЩЛиЪеЮяЃЌBЮЊГјгрРЌЛјЃЌCЮЊгаКІРЌЛјЃЌDЮЊЦфЫћРЌЛјЃЉ
ИљОнЭМБэНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉдкГщбљЪ§ОнжаЃЌВњЩњЕФгаКІРЌЛјЙВЖрЩйЖжЃП
ЃЈ2ЃЉЧыНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉЕїВщЗЂЯжЃЌдкПЩЛиЪеЮяжаЫмСЯРрРЌЛјеМ![]() ЃЌУПЛиЪе1ЖжЫмСЯРрРЌЛјПЩЛёЕУ0.7ЖжЖўМЖдСЯЃЎМйЩшИУГЧЪаУПдТВњЩњЕФЩњЛюРЌЛјЮЊ5000ЖжЃЌЧвШЋВПЗжРрДІРэЃЌФЧУДУПдТЛиЪеЕФЫмСЯРрРЌЛјПЩвдЛёЕУЖрЩйЖжЖўМЖдСЯЃП
ЃЌУПЛиЪе1ЖжЫмСЯРрРЌЛјПЩЛёЕУ0.7ЖжЖўМЖдСЯЃЎМйЩшИУГЧЪаУПдТВњЩњЕФЩњЛюРЌЛјЮЊ5000ЖжЃЌЧвШЋВПЗжРрДІРэЃЌФЧУДУПдТЛиЪеЕФЫмСЯРрРЌЛјПЩвдЛёЕУЖрЩйЖжЖўМЖдСЯЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєa+b=2ЃЌдђГЦaгыbЪЧЙигк1ЕФЦНКтЪ§ЃЎ
ЃЈ1ЃЉ3гыЁЁ ЁЁЪЧЙигк1ЕФЦНКтЪ§ЃЌ5Љ![]() гыЁЁ ЁЁЪЧЙигк1ЕФЦНКтЪ§ЃЛ
гыЁЁ ЁЁЪЧЙигк1ЕФЦНКтЪ§ЃЛ
ЃЈ2ЃЉШєЃЈm+![]() ЃЉЁСЃЈ1Љ
ЃЉЁСЃЈ1Љ![]() ЃЉ=Љ5+3
ЃЉ=Љ5+3![]() ЃЌХаЖЯm+
ЃЌХаЖЯm+![]() гы5Љ
гы5Љ![]() ЪЧЗёЪЧЙигк1ЕФЦНКтЪ§ЃЌВЂЫЕУїРэгЩЃЎ
ЪЧЗёЪЧЙигк1ЕФЦНКтЪ§ЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
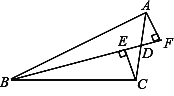
ЁОЬтФПЁПШчЭМЃЌвбжЊBDЮЊЁїABCЕФжаЯпЃЌCEЁЭBDгкEЃЌAFЁЭBDгкFЃЎгкЪЧаЁАзЫЕЃК
ЁАBE+BF=2BDЁБЃЎФуШЯЮЊЫћЕФХаЖЯЖдТ№ЃПЮЊЪВУДЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌAЃЈ1ЃЌ2ЃЉЃЌBЃЈ3ЃЌ1ЃЉЃЌCЃЈЉ2ЃЌЉ1ЃЉЃЎ
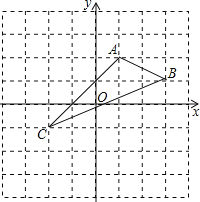
ЃЈ1ЃЉдкЭМжазїГіЁїABCЙигкyжсЖдГЦЕФЁїA1B1C1ЃЎ
ЃЈ2ЃЉаДГіA1ЃЌB1ЃЌC1ЕФзјБъЃЈжБНгаДГіД№АИЃЉЃЌA1 ЃЛB1 ЃЛC1 ЃЎ
ЃЈ3ЃЉЁї A1B1C1ЕФУцЛ§ЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИјГіЯТСаХаЖЯЃКЂйдкЪ§жсЩЯЃЌдЕуСНХдЕФСНИіЕуЫљБэЪОЕФЪ§ЖМЪЧЛЅЮЊЯрЗДЪ§ЃЛЂкШЮКЮе§Ъ§БиЖЈДѓгкЫќЕФЕЙЪ§ЃЛЂл5abЃЌ ![]() ЃЌ
ЃЌ ![]() ЖМЪЧећЪНЃЛЂмx2Љxy+y2ЪЧАДзжФИyЕФЩ§УнХХСаЕФЖрЯюЪНЃЌЦфжаХаЖЯе§ШЗЕФЪЧЃЈ ЃЉ
ЖМЪЧећЪНЃЛЂмx2Љxy+y2ЪЧАДзжФИyЕФЩ§УнХХСаЕФЖрЯюЪНЃЌЦфжаХаЖЯе§ШЗЕФЪЧЃЈ ЃЉ
A.ЂйЂк
B.ЂкЂл
C.ЂлЂм
D.ЂйЂм
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com