
【题目】定义:圆心在三角形的一边上,与另一边相切,且经过三角形一个顶点(非切点)的圆,称为这个三角形圆心所在边上的“伴随圆”.
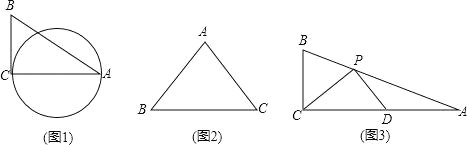
(1)如图1,△ABC中,∠C=90°,AB=5,BC=3,则AC边上的伴随圆的半径为 .
(2)如图2,已知等腰△ABC,AB=AC=5,BC=6,画草图并直接写出它的所有伴随圆的半径.
(3)如图3,△ABC中,∠ACB=90°,点P在边AB上,AP=2BP,D为AC中点,且∠CPD=90°.
①求证:△CPD的外接圆是△ABC某一条边上的伴随圆;
②求cos∠PDC的值.
【答案】(1)2.(2)△ABC的伴随圆的半径分为![]() 或
或![]() 或
或![]() .(3)cos∠PDC=
.(3)cos∠PDC=![]() .
.
【解析】
试题分析:(1)先依据勾股定理求得AC的长,然后依据切线的性质可知AC为圆的直径,故此可求得△BAC的伴随圆的半径等于AC的一半;
(2)当O在BC上时,连接OD,过点A作AE⊥BC.由等腰三角形的性质和勾股定理求得AE=4,依据切线的性质可证明OD⊥AB,接下来证明△ODB∽△AEB,由相似三角形的性质可求得圆O的半径;当O在AB上且圆O与BC相切时,连接OD、过点A作AE⊥BC,垂足为E.先证明△BOD∽△BAE,由相似三角形的性质可求得圆O的半径,当O在AB上且圆O与AC相切时,连接OD、过点B作BF⊥AC,过点A作AE⊥BC,垂足为E.先依据面积法求得BF的长,然后再证明△AOD∽△ABF,由相似三角形的性质可求得圆O的半径;
(3)①连接OB、OP,先证明![]() ,从而得到PD∥OB,于是可得到∠1=∠4,接下来证明△BCO≌△BPO,从而可证明∠BPO=90°;②设圆O的半径为r,依据勾股定理定理依据求得PA、BC、OB的长,从而可求得cos∠1=
,从而得到PD∥OB,于是可得到∠1=∠4,接下来证明△BCO≌△BPO,从而可证明∠BPO=90°;②设圆O的半径为r,依据勾股定理定理依据求得PA、BC、OB的长,从而可求得cos∠1=![]() 接下来,由∠PDC=∠1可求得cos∠PDC=的值.
接下来,由∠PDC=∠1可求得cos∠PDC=的值.
试题解析:(1)∵∠C=90°,AB=5,BC=3,
∴AC=![]() =4.
=4.
∵BC是圆的切线,∠BCA=90°,
∴AC为圆的直径.
∴AC边上的半随圆的半径为2.
故答案为:2.
(2)当O在BC上时,如图(1)所示:连接OD,过点A作AE⊥BC.

∵AB=AC,AE⊥BC,
∴BE=EC=3.
在△AEB中,由勾股定理可知AE=![]() =4.
=4.
∵AB与⊙O相切,
∴OD⊥AB.
∴∠BDO=∠BEA=90°.
又∵∠OBD=∠EBA,
∴△ODB∽△AEB.
∴![]() .
.
设⊙O的半径为r.在OB=6﹣r.
∴![]() .
.
∴r=![]() .
.
∴△ABC的BC边上的伴随圆的半径为![]() .
.
当O在AB上时,如图(2),连接OD、过点A作AE⊥BC,垂足为E.

∵BC与⊙O相切,∴OD⊥BC.又∵AE⊥BC,
∴OD∥AE.∴△BOD∽△BAE.
∴![]() .
.
设⊙O的半径为r,则OB=5﹣r.∴![]() .∴r=
.∴r=![]() .
.
如图(3)所示:连接OD、过点B作BF⊥AC,过点A作AE⊥BC,垂足为E.

∵S△ABC=![]() BCAE=
BCAE=![]() ACBF,∴
ACBF,∴![]() ×6×4=
×6×4=![]() ×5×BF.∴BF=4.8.
×5×BF.∴BF=4.8.
∵AC与⊙O相切,∴DO⊥AC.∴DO∥BF.
∴△AOD∽△ABF.∴![]() 即
即![]() .∴r=
.∴r=![]() .
.
综上所述,△ABC的伴随圆的半径分为![]() 或
或![]() 或
或![]() .
.
(3)①证明:如图(4)连接OP、OB.

∵△CPD为直角三角形,
∴△CPD的外接圆圆心O在CD中点.
设⊙O的半径为r,则DC=2r,OA=3r.∴![]() .∵PA=2BP,
.∵PA=2BP,
∴![]() .∴
.∴![]() .∴PD∥OB.∴∠1=∠2,∠3=∠4.
.∴PD∥OB.∴∠1=∠2,∠3=∠4.
又∵∠3=∠2,∴∠1=∠4.在△BCO和△BPO中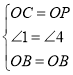 ,∴△BCO≌△BPO.
,∴△BCO≌△BPO.
∴∠BPO=∠BCO=90°.∴AB是圆O的切线.
∴△CPD的外接圆是△ABC某一条边上的伴随圆.
②如图(4)设圆O的半径为r.
∵在Rt△OAP中,OA=3r,OP=r,
∴PA=![]() =2
=2![]() r.
r.
∴AB=3![]() r.
r.
∵在Rt△ABC中,AC=4r,AB=3![]() r,
r,
∴BC=![]() =
=![]() a.
a.
∵在Rt△OBC中,OC=r,BC=![]() r,
r,
∴OB=![]() =
=![]() r.
r.
∴cos∠1=![]() =
=![]() =
=![]() .
.
∵∠PDC=∠1,
∴cos∠PDC=![]() .
.


科目:初中数学 来源: 题型:
【题目】下面关于平行四边形的说法中错误的是( )
A. 平行四边形的两条对角线相等
B. 平行四边形的两条对角线互相平分
C. 平行四边形的对角相等
D. 平行四边形的对边相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)某校为表彰在美术展览活动中获奖的同学,决定购买一些水笔和颜料盒作为奖品,请你根据图中所给的信息,解答下列问题:
(1)求出每个颜料盒、每支水笔各多少元?
(2)若学校计划购买颜料盒和水笔共20个,所用费用不超过340元,则颜料盒至多购买多少个?
(3)恰逢商店举行优惠促销活动,具体办法如下:颜料盒按七折优惠,水笔10支以上超出部分按八折优惠,若学校决定购买同种数量的同一奖品,并且该奖品的数量超过10件,请你帮助分析,购买颜料盒合算还是购买水笔合算.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考英语听力测试期间T需要杜绝考点周围的噪音.如图,点A是某市一中考考点,在位于考点南偏西15°方向距离500米的C点处有一消防队.在听力考试期间,消防队突然接到报警电话,消防车需沿北偏东75°方向的公路CF前往救援.已知消防车的警报声传播半径为400米,若消防车的警报声对听力测试造成影响,则消防车必须改道行驶.试问:消防车是否需要改道行驶?
说明理由.(![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+3交x轴于A(﹣1,0)和B(5,0),交y轴于点C,点D是线段OB上一动点,连接CD,将CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF,CE交于点G.
(1)求抛物线解析式;
(2)求线段DF的长;
(3)当DG=![]() 时,
时,
①求tan∠CGD的值;
②试探究在x轴上方的抛物线上,是否存在点P,使∠EDP=45°?若存在,请写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.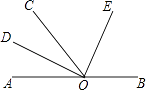
(1)∠AOD的余角是 , ∠COD的余角是
(2)OE是∠BOC的平分线吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com