

| A���dz��˽� | 5% |
| B���Ƚ��˽� | m |
| C�������˽� | 45% |
| D�����˽� | n |
���� ��1��ͼ����ͼ����A�ȼ���D�ȼ����������Ӧ�İٷֱȾ���֪�����ι�ʽ���ٷֱ�=$\frac{�������ijһ�ȼ�������}{�������������}��$100%�Ϳ�����⣻
��2����������Ӧ��Բ�ĽǵĶ���=360���D�ȼ���ռ�İٷֱȣ���ֵ���㼴�ɣ�
��3��D�ȼ�����=400-20-60-180=140��ͼ���в�ȫ���ɣ�
��� �⣺��1��20��5%=400���ˣ���m=60��400��100%=15%��n=��400-20-60-180����400��100%=35%
�������β�������ѧ������400�ˣ�m=15%��n=35%
��2��360���35%=126�㣬
����ͼ2��ʾ������ͳ��ͼ��D������������Ӧ��Բ�Ľ�126�㣮
��3����ȫͼ��ʾ��������ͳ��ͼ����ͼ��ʾ��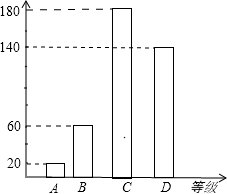
���� ���⿼��������ͳ��ͼ������ͳ��ͼ��ͳ�Ʊ���֪ʶ�㣬����Ĺؼ��������ͼ����ñ�Ҫ�����ݣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪A��F��E��C��ͬһֱ���ϣ�AB��CD����ABE=��CDF��AF=CE��
��ͼ����֪A��F��E��C��ͬһֱ���ϣ�AB��CD����ABE=��CDF��AF=CE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com