Question

【题目】如图，在中， 是边上的中线， 是的中点，过点作的平行线交的延长线于点，连结和．

（1）求证：四边形是平行四边形；

（2）若，试判断四边形的形状，并证明你的结论；

（3）是什么三角形时，四边形是正方形，请说明理由.

Answer 1

【答案】（1）证明见解析；

（2）若AB⊥AC，则四边形ADCF是菱形，证明见解析；

（3）当△ABC是以BC为斜边的等腰直角三角形时，四边形ADCF是正方形.理由见解析.

【解析】试题分析：（1）连接DF，由AAS证明△AFE≌△DBE，得出EF=EB且AE=DE，即可得出答案；

（2）根据平行四边形的判定得出平行四边形ADCF，求出AD=CD，根据菱形的判定得出即可；

（3）根据等腰三角形性质求出AD⊥BC，得出∠ADC=90°，根据正方形的判定得出即可．

试题解析：（1）

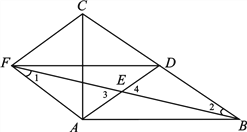
∵AF∥BC，

∴∠1=∠2，

在△AEF和△DEB中， ，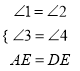

∴△AEF≌△DEB（AAS），

∴EF=EB且AE=DE，

∴四边形ABDF是平行四边形；

（2）若AB⊥AC，则四边形ADCF是菱形，证明如下：

∵四边形ABDF是平行四边形，

∴AB∥FD 且 AF=BD，

又∵BD=CD，

∴AF=DC且 AF∥CD，

∴四边形ADCF是平行四边形，

∵AB∥FD，AB⊥AC，

∴FD⊥AC，

∴平行四边形ADCF是菱形；

（3）当△ABC是以BC为斜边的等腰直角三角形时，四边形ADCF是正方形.理由是：

当∠BAC=90o时，由（2）得：四边形ADCF是菱形，

由（1）知：四边形ABDF是平行四边，

∴AB=FD，

从而当AB=AC时有AC=FD，

∴菱形ADCF是正方形.