Question

如图，已知AB=AC，以AB为直径的圆O交边BC于点D，过点D作DE⊥AC，垂足为点E．
（1）求证：DE是圆O的切线；
（2）如果∠BAC=120°，求证：DE=BC．

Answer 1

（1）证明：
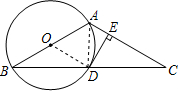
连接OD、AD，
∵AB是⊙O直径，
∴∠ADB=90°，
∴AD⊥BC，
∵AB=AC，
∴BD=DC（三线合一定理），
∵BO=OA，
∴OD∥AC，
∵DE⊥AC，
∴DE⊥OD，
∵OD是半径，
∴DE是圆O的切线；

（2）证明：∵AB=AC，∠BAC=120°，
∴∠B=∠C=（180°-∠BAC）=30°，
∵DE⊥AC，
∴∠CED=90°，
∴DE=DC，
∵DC=BD=BC，
∴DE=BC．
分析：（1）连接OD、AD，根据圆周角定理求出∠ADB=90°，根据等腰三角形的三线合一得出BD=DC，求出OD是△BAC的中位线，推出OD∥AC，推出DE⊥OD，根据切线的判定定理推出即可；
（2）根据等腰三角形性质和三角形的内角和定理求出∠C的度数，根据含30度角的直角三角形性质求出DE=DC，根据DC=BC，代入求出即可．
点评：本题综合性比较强，考查了等腰三角形的性质和判定，切线的判定，含30度角的直角三角形性质，三角形的中位线定理等，注意：含30度角所对的直角边等于斜边的一半．