
分析 根据根与系数的关系得到x1+x2=$\frac{5}{2}$,x1x2=$\frac{1}{2}$,再经过代数式的变形得到x12+x22=(x1+x2)2-2x1x2,$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$,然后利用整体代入的方法计算.
解答 解:根据题意得x1+x2=$\frac{5}{2}$,x1x2=$\frac{1}{2}$,
所以x12+x22=(x1+x2)2-2x1x2=($\frac{5}{2}$)2-2×$\frac{1}{2}$=$\frac{21}{4}$;
$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{\frac{5}{2}}{\frac{1}{2}}$=5.
故答案为$\frac{21}{4}$,5.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.


科目:初中数学 来源: 题型:选择题
| A. | 8的立方根是±2 | B. | $-\frac{1}{2}$是$-\frac{1}{6}$的立方根 | ||
| C. | 负数没有立方根 | D. | $\root{3}{-64}$=-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
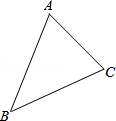 画图并讨论:已知△ABC,如图所示,要求画一个三角形,使它与△ABC有一个公共的顶点C,并且与△ABC全等.
画图并讨论:已知△ABC,如图所示,要求画一个三角形,使它与△ABC有一个公共的顶点C,并且与△ABC全等.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
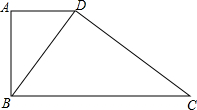 直角梯形ABCD中,AD∥BC,BA⊥AD,∠BDC=90°,其中AD=4米,BC=9米,则BD的长度为( )
直角梯形ABCD中,AD∥BC,BA⊥AD,∠BDC=90°,其中AD=4米,BC=9米,则BD的长度为( )| A. | 12米 | B. | 13米 | C. | 5米 | D. | 6米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com